Statistical arbitrage exploits short-term price inefficiencies by using quantitative models to identify and capitalize on mean-reverting securities relationships. Statistical factor modeling decomposes asset returns into underlying factors such as market, size, and value to explain systematic risks and improve portfolio optimization. Discover how these advanced trading strategies enhance risk-adjusted returns and drive market efficiency.
Why it is important
Understanding the difference between statistical arbitrage and statistical factor modeling is crucial for traders to optimize risk-adjusted returns and refine asset allocation strategies. Statistical arbitrage involves exploiting short-term pricing inefficiencies using mean-reversion techniques, whereas statistical factor modeling focuses on identifying underlying factors driving asset returns over longer horizons. Mastery of these concepts enhances portfolio diversification and improves predictive accuracy in market behavior. Accurate differentiation supports tailored strategy development and effective risk management in volatile trading environments.
Comparison Table
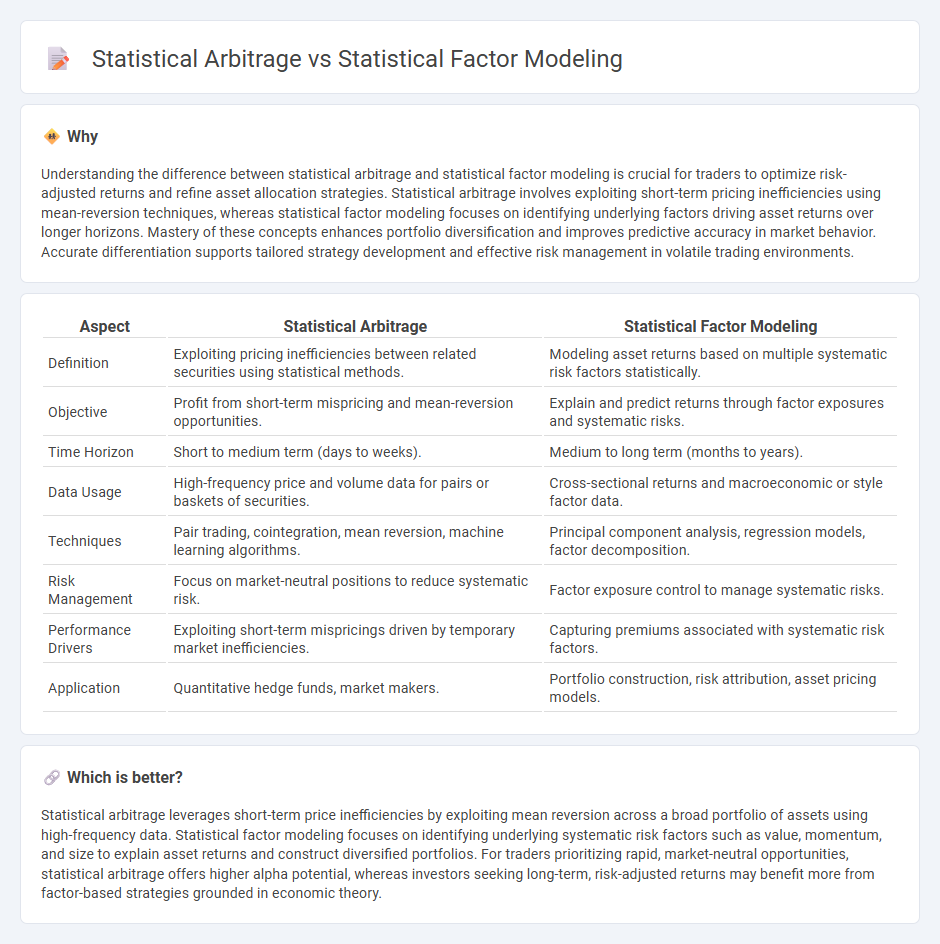
| Aspect | Statistical Arbitrage | Statistical Factor Modeling |
|---|---|---|
| Definition | Exploiting pricing inefficiencies between related securities using statistical methods. | Modeling asset returns based on multiple systematic risk factors statistically. |
| Objective | Profit from short-term mispricing and mean-reversion opportunities. | Explain and predict returns through factor exposures and systematic risks. |
| Time Horizon | Short to medium term (days to weeks). | Medium to long term (months to years). |
| Data Usage | High-frequency price and volume data for pairs or baskets of securities. | Cross-sectional returns and macroeconomic or style factor data. |
| Techniques | Pair trading, cointegration, mean reversion, machine learning algorithms. | Principal component analysis, regression models, factor decomposition. |
| Risk Management | Focus on market-neutral positions to reduce systematic risk. | Factor exposure control to manage systematic risks. |
| Performance Drivers | Exploiting short-term mispricings driven by temporary market inefficiencies. | Capturing premiums associated with systematic risk factors. |
| Application | Quantitative hedge funds, market makers. | Portfolio construction, risk attribution, asset pricing models. |
Which is better?
Statistical arbitrage leverages short-term price inefficiencies by exploiting mean reversion across a broad portfolio of assets using high-frequency data. Statistical factor modeling focuses on identifying underlying systematic risk factors such as value, momentum, and size to explain asset returns and construct diversified portfolios. For traders prioritizing rapid, market-neutral opportunities, statistical arbitrage offers higher alpha potential, whereas investors seeking long-term, risk-adjusted returns may benefit more from factor-based strategies grounded in economic theory.
Connection
Statistical arbitrage leverages quantitative techniques to identify pricing inefficiencies in financial markets, relying heavily on statistical factor modeling to isolate and measure risk factors driving asset returns. These models decompose returns into systematic and idiosyncratic components, enabling traders to predict mean-reversion and generate alpha through market-neutral portfolios. Effective integration of statistical factor models enhances arbitrage strategies by improving signal accuracy and risk management in dynamic market conditions.
Key Terms
**Statistical Factor Modeling:**
Statistical factor modeling identifies underlying factors driving asset returns by analyzing historical data to explain and predict price movements through multiple risk factors. It enhances portfolio construction by isolating systematic risks, improving diversification, and optimizing asset allocation based on factor exposures. Explore how statistical factor modeling empowers quantitative investment decisions and risk management strategies.
Principal Component Analysis (PCA)
Statistical factor modeling utilizes Principal Component Analysis (PCA) to identify latent factors driving asset returns by decomposing covariance matrices, enhancing risk management and portfolio construction. Statistical arbitrage leverages these PCA-derived factors to exploit mean-reverting price patterns and market inefficiencies through systematic trading strategies. Explore how integrating PCA in both approaches can optimize quantitative investment performance.
Factor Loadings
Factor loadings in statistical factor modeling quantify the sensitivity of asset returns to underlying common factors, enabling investors to identify and isolate systematic risk drivers. In statistical arbitrage, these factor loadings inform portfolio construction by capturing predictable relationships among assets, facilitating the exploitation of pricing inefficiencies. Discover how deep analysis of factor loadings enhances both risk management and alpha generation strategies.
Source and External Links
Robust high dimensional factor models with applications to ... - Factor models are powerful statistical tools widely used for dependent measurements across fields like genomics, neuroscience, economics, and finance, especially in high-dimensional settings, with PCA being a central method for estimation and inference.
An Introduction to Factor Analysis: Reducing Variables - Factor analysis is a sophisticated statistical method used to reduce many observed variables into a smaller set of latent factors, primarily via PCA, focusing on extracting common variance and underlying relationships.
Factor analysis - Statistical factor modeling explains variability among observed correlated variables by mapping them to fewer unobserved common factors through a factor loading matrix, accounting also for unique error terms in each observation.
 dowidth.com
dowidth.com