Algorithmic arbitrage uses automated systems to exploit price discrepancies across different markets with high-speed trading algorithms, enhancing profitability and reducing human error. Options pricing models, such as the Black-Scholes and Binomial models, provide mathematical frameworks to estimate fair values and manage risk for derivatives trading. Explore how these strategies combine technology and quantitative analysis to optimize trading decisions.
Why it is important
Understanding the difference between algorithmic arbitrage and options pricing models is crucial for traders to effectively manage risk and optimize profit strategies. Algorithmic arbitrage exploits price discrepancies across markets using automated trading systems, while options pricing models, such as Black-Scholes, estimate theoretical option values to guide investment decisions. Mastering both concepts enables precise execution of trades and improves the accuracy of market forecasts. This knowledge enhances decision-making in volatile trading environments and maximizes financial returns.
Comparison Table
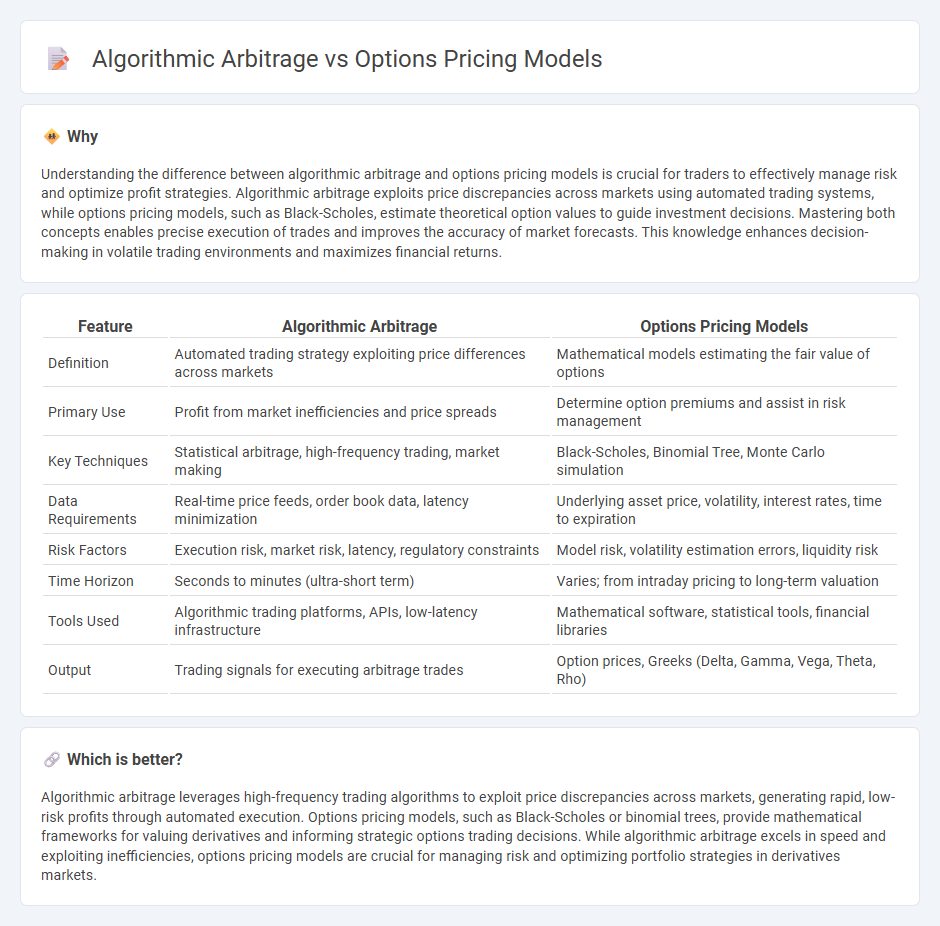
| Feature | Algorithmic Arbitrage | Options Pricing Models |
|---|---|---|
| Definition | Automated trading strategy exploiting price differences across markets | Mathematical models estimating the fair value of options |
| Primary Use | Profit from market inefficiencies and price spreads | Determine option premiums and assist in risk management |
| Key Techniques | Statistical arbitrage, high-frequency trading, market making | Black-Scholes, Binomial Tree, Monte Carlo simulation |
| Data Requirements | Real-time price feeds, order book data, latency minimization | Underlying asset price, volatility, interest rates, time to expiration |
| Risk Factors | Execution risk, market risk, latency, regulatory constraints | Model risk, volatility estimation errors, liquidity risk |
| Time Horizon | Seconds to minutes (ultra-short term) | Varies; from intraday pricing to long-term valuation |
| Tools Used | Algorithmic trading platforms, APIs, low-latency infrastructure | Mathematical software, statistical tools, financial libraries |
| Output | Trading signals for executing arbitrage trades | Option prices, Greeks (Delta, Gamma, Vega, Theta, Rho) |
Which is better?
Algorithmic arbitrage leverages high-frequency trading algorithms to exploit price discrepancies across markets, generating rapid, low-risk profits through automated execution. Options pricing models, such as Black-Scholes or binomial trees, provide mathematical frameworks for valuing derivatives and informing strategic options trading decisions. While algorithmic arbitrage excels in speed and exploiting inefficiencies, options pricing models are crucial for managing risk and optimizing portfolio strategies in derivatives markets.
Connection
Algorithmic arbitrage leverages advanced options pricing models such as Black-Scholes and binomial trees to identify mispricings in real-time market data. These models provide theoretical option values that algorithmic systems compare against current market prices to execute profitable trades automatically. Accurate options pricing directly enhances the efficiency and success rate of algorithmic arbitrage strategies in financial markets.
Key Terms
**Options Pricing Models:**
Options pricing models, such as the Black-Scholes and Binomial models, provide mathematical frameworks to estimate the fair value of options by analyzing factors like underlying asset price, volatility, time to expiration, and interest rates. These models help traders and investors assess risk and make informed decisions by predicting option premiums and identifying mispriced securities. Explore more to understand how these models impact trading strategies and risk management techniques.
Black-Scholes Model
The Black-Scholes model revolutionizes options pricing by providing a mathematical framework to estimate fair option values based on parameters like stock price, strike price, volatility, time to expiration, and risk-free interest rate. Algorithmic arbitrage, in contrast, leverages high-frequency trading algorithms to exploit price discrepancies across markets, often incorporating real-time data and complex statistical models beyond Black-Scholes assumptions. Explore deeper insights into how the Black-Scholes model underpins options pricing while algorithmic arbitrage strategies enhance market efficiency.
Implied Volatility
Options pricing models such as Black-Scholes rely heavily on implied volatility to estimate fair option values by reflecting market expectations of future price fluctuations. Algorithmic arbitrage strategies exploit discrepancies in implied volatility across different option contracts or markets to generate riskless profits. Explore how advanced modeling of implied volatility enhances both options pricing precision and arbitrage opportunities.
Source and External Links
Options Pricing Models - Financial Edge - Options pricing models calculate the value of an options contract using variables like intrinsic and time value; well-known models include the Black-Scholes and Binomial Pricing models, which estimate whether options are in-the-money or out-of-the-money.
Option Pricing Models - Definition, Types, How to Use - These mathematical models estimate the theoretical fair value of options using variables such as exercise style (American or European), risk-neutral probabilities, and known inputs, helping traders adjust strategies.
CHAPTER 5 OPTION PRICING THEORY AND MODELS - The binomial pricing model, an intuitive discrete-time framework, converges to the continuous-time Black-Scholes model under certain assumptions about price changes; both are key in understanding option valuation and factors like time to expiration and price volatility.
 dowidth.com
dowidth.com