Quantum advantage represents the point where quantum computers solve problems faster than classical ones, with Grover's algorithm offering a quadratic speedup for unstructured search tasks by reducing search from O(N) to O(N). This algorithm exemplifies quantum computing's potential in optimizing search operations and database queries, showcasing practical benefits over classical counterparts. Explore deeper into how Grover's algorithm paves the way for realizing quantum advantage in computational complexity.
Why it is important
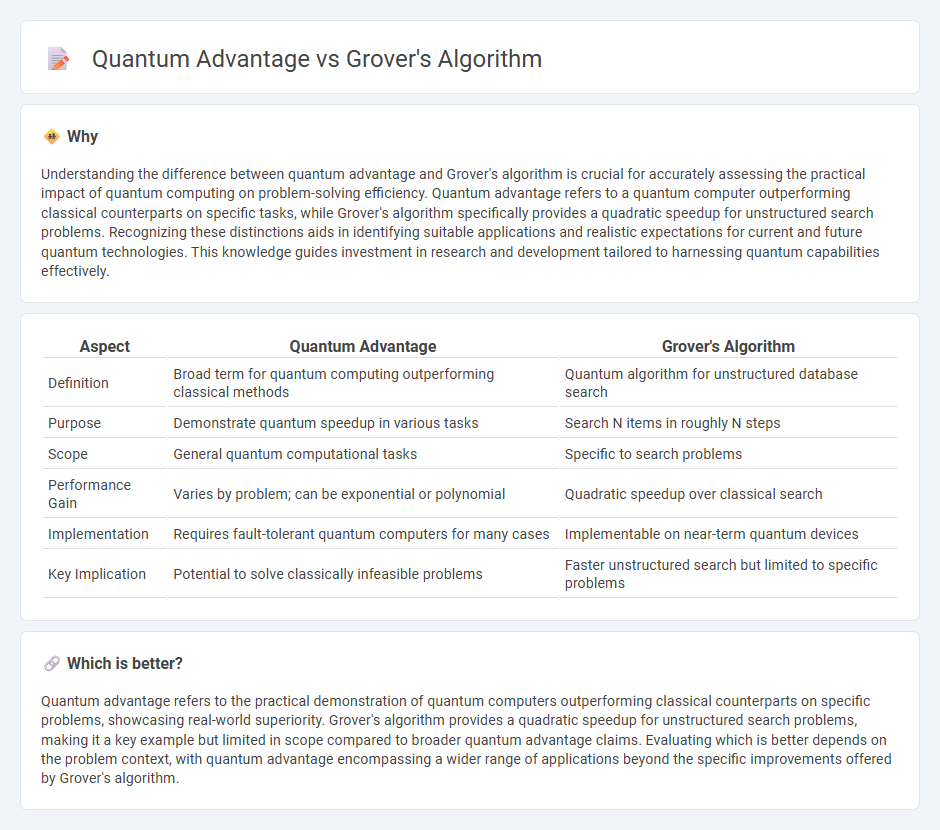
Understanding the difference between quantum advantage and Grover's algorithm is crucial for accurately assessing the practical impact of quantum computing on problem-solving efficiency. Quantum advantage refers to a quantum computer outperforming classical counterparts on specific tasks, while Grover's algorithm specifically provides a quadratic speedup for unstructured search problems. Recognizing these distinctions aids in identifying suitable applications and realistic expectations for current and future quantum technologies. This knowledge guides investment in research and development tailored to harnessing quantum capabilities effectively.
Comparison Table
| Aspect | Quantum Advantage | Grover's Algorithm |
|---|---|---|
| Definition | Broad term for quantum computing outperforming classical methods | Quantum algorithm for unstructured database search |
| Purpose | Demonstrate quantum speedup in various tasks | Search N items in roughly N steps |
| Scope | General quantum computational tasks | Specific to search problems |
| Performance Gain | Varies by problem; can be exponential or polynomial | Quadratic speedup over classical search |
| Implementation | Requires fault-tolerant quantum computers for many cases | Implementable on near-term quantum devices |
| Key Implication | Potential to solve classically infeasible problems | Faster unstructured search but limited to specific problems |
Which is better?
Quantum advantage refers to the practical demonstration of quantum computers outperforming classical counterparts on specific problems, showcasing real-world superiority. Grover's algorithm provides a quadratic speedup for unstructured search problems, making it a key example but limited in scope compared to broader quantum advantage claims. Evaluating which is better depends on the problem context, with quantum advantage encompassing a wider range of applications beyond the specific improvements offered by Grover's algorithm.
Connection
Quantum advantage is demonstrated when quantum computers outperform classical ones in specific tasks, and Grover's algorithm exemplifies this by providing a quadratic speedup for unstructured search problems. Grover's algorithm leverages quantum superposition and interference to search an unsorted database of N items in approximately N operations, compared to classical O(N) time. This significant improvement showcases a clear instance where quantum computation achieves an advantage over classical algorithms in practical applications.
Key Terms
Quantum Speedup
Grover's algorithm offers a quadratic quantum speedup for unstructured search problems, providing a solution in O(N) time compared to O(N) classically. This quantum speedup exemplifies the potential of quantum advantage, where quantum hardware outperforms classical counterparts in specific computational tasks. Explore how Grover's algorithm leverages amplitude amplification to achieve this acceleration and its implications for quantum computing breakthroughs.
Oracle Search
Grover's algorithm exemplifies quantum advantage by providing a quadratic speedup for unstructured database searches using an oracle, reducing complexity from O(N) to O(N). The algorithm leverages quantum superposition and amplitude amplification to efficiently identify target entries within a search space. Explore the underlying principles and practical implementations of Grover's algorithm to better understand its impact on quantum computing advancements.
Superposition
Grover's algorithm leverages the principle of superposition to search unsorted databases quadratically faster than classical algorithms by evaluating multiple states simultaneously. This quantum advantage arises from superposition enabling parallel computation over a vast search space, reducing query complexity from O(N) to O(N). Explore how superposition fundamentally enhances quantum computing efficiency and unlocks practical speedups.
Source and External Links
Introduction to Grover's Algorithm - GeeksforGeeks - Grover's algorithm is a quantum algorithm that solves unstructured search problems by amplifying the probability amplitude of the desired state through repeated applications of a quantum operator, returning the marked element with high probability after about \(\sqrt{N}\) steps.
Grover's algorithm - Wikipedia - Grover's algorithm is a quantum search algorithm that finds with high probability the unique input to a black box function using \(O(\sqrt{N})\) queries, achieving a quadratic speedup over classical methods for unstructured search problems.
But what is quantum computing? (Grover's Algorithm) - YouTube - Grover's algorithm works by iteratively rotating the quantum state vector toward the solution using a specific sequence of quantum operations, with the optimal number of iterations being approximately \(\frac{\pi}{4}\sqrt{N}\).
 dowidth.com
dowidth.com