Graph Neural Networks (GNNs) excel in modeling complex relational data by leveraging graph structures, enabling advanced tasks like node classification and link prediction with high accuracy. Support Vector Machines (SVMs) offer robust performance in classification problems with clear hyperplane separation but may struggle with non-Euclidean data complexities inherent in graphs. Explore the nuances and applications of GNNs versus SVMs to understand their strengths in modern machine learning.
Why it is important
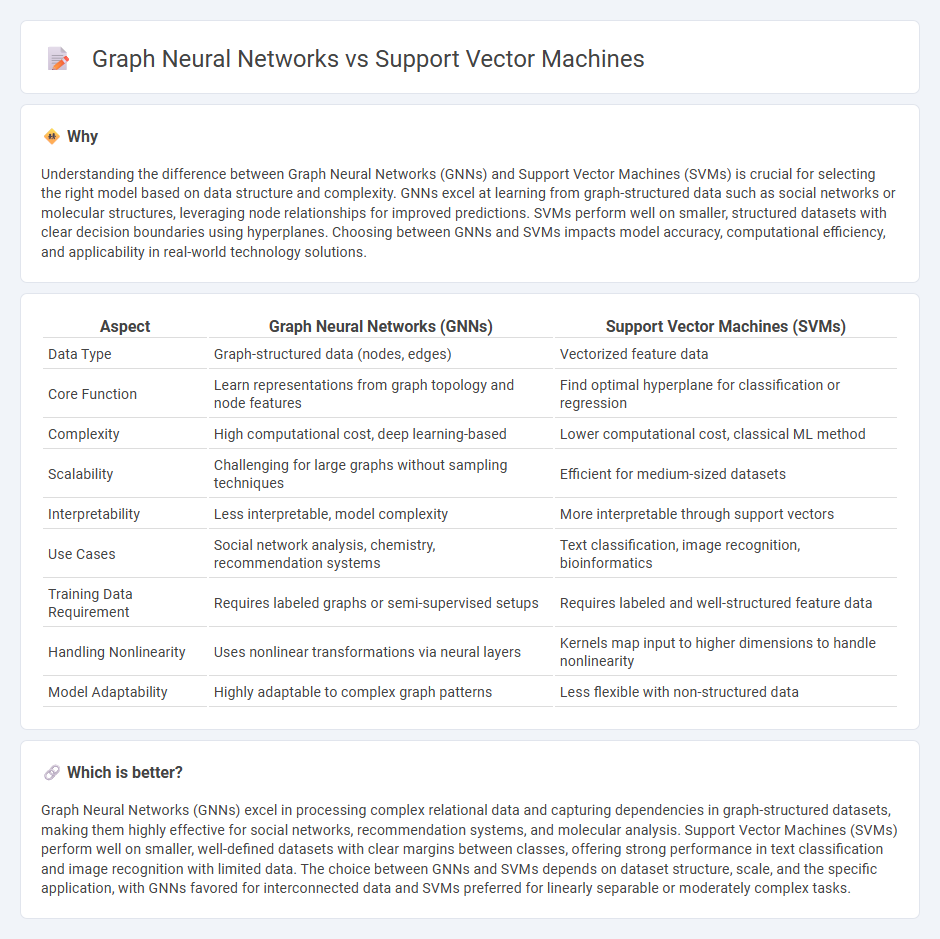
Understanding the difference between Graph Neural Networks (GNNs) and Support Vector Machines (SVMs) is crucial for selecting the right model based on data structure and complexity. GNNs excel at learning from graph-structured data such as social networks or molecular structures, leveraging node relationships for improved predictions. SVMs perform well on smaller, structured datasets with clear decision boundaries using hyperplanes. Choosing between GNNs and SVMs impacts model accuracy, computational efficiency, and applicability in real-world technology solutions.
Comparison Table
| Aspect | Graph Neural Networks (GNNs) | Support Vector Machines (SVMs) |
|---|---|---|
| Data Type | Graph-structured data (nodes, edges) | Vectorized feature data |
| Core Function | Learn representations from graph topology and node features | Find optimal hyperplane for classification or regression |
| Complexity | High computational cost, deep learning-based | Lower computational cost, classical ML method |
| Scalability | Challenging for large graphs without sampling techniques | Efficient for medium-sized datasets |
| Interpretability | Less interpretable, model complexity | More interpretable through support vectors |
| Use Cases | Social network analysis, chemistry, recommendation systems | Text classification, image recognition, bioinformatics |
| Training Data Requirement | Requires labeled graphs or semi-supervised setups | Requires labeled and well-structured feature data |
| Handling Nonlinearity | Uses nonlinear transformations via neural layers | Kernels map input to higher dimensions to handle nonlinearity |
| Model Adaptability | Highly adaptable to complex graph patterns | Less flexible with non-structured data |
Which is better?
Graph Neural Networks (GNNs) excel in processing complex relational data and capturing dependencies in graph-structured datasets, making them highly effective for social networks, recommendation systems, and molecular analysis. Support Vector Machines (SVMs) perform well on smaller, well-defined datasets with clear margins between classes, offering strong performance in text classification and image recognition with limited data. The choice between GNNs and SVMs depends on dataset structure, scale, and the specific application, with GNNs favored for interconnected data and SVMs preferred for linearly separable or moderately complex tasks.
Connection
Graph neural networks (GNNs) and Support Vector Machines (SVMs) are connected through their applications in structured data analysis, where GNNs excel in learning representations from graph-structured inputs, enabling effective node classification or link prediction. SVMs can utilize these learned embeddings from GNNs as feature vectors for large-margin classification, improving decision boundaries in high-dimensional spaces. Combining GNNs' graph representation capabilities with the robust classification power of SVMs enhances performance in tasks like bioinformatics, social network analysis, and recommendation systems.
Key Terms
Hyperplane (Support Vector Machines)
Support Vector Machines (SVMs) utilize a hyperplane to separate data points with maximum margin in high-dimensional spaces, enabling effective classification even with limited samples. The hyperplane is defined by support vectors, which are the critical data points closest to the decision boundary, optimizing the model's generalization capabilities. Explore deeper insights into how hyperplanes in SVMs compare with the relational learning mechanisms of graph neural networks.
Node Embeddings (Graph Neural Networks)
Support Vector Machines (SVMs) rely on kernel methods to classify data by maximizing the margin between classes but lack inherent ability to capture complex graph structures, making them less effective for node embedding tasks. Graph Neural Networks (GNNs), including variants like Graph Convolutional Networks (GCNs) and Graph Attention Networks (GATs), directly learn node embeddings by aggregating feature information from neighbors, enabling superior performance in tasks such as node classification and link prediction. Explore how GNNs transform graph data into expressive embeddings and outperform traditional SVMs in graph-based machine learning.
Kernel Trick (Support Vector Machines)
Support Vector Machines utilize the Kernel Trick to transform input data into higher-dimensional spaces, enabling linear separation of complex, non-linear patterns by implicitly computing inner products without explicit mapping. In contrast, Graph Neural Networks process relational data through message passing and aggregation mechanisms, capturing structural dependencies without relying on kernel functions. Explore further how these approaches tackle non-linear problems to enhance machine learning model performance.
Source and External Links
1.4. Support Vector Machines - Scikit-learn - Support Vector Machines (SVMs) are supervised learning methods for classification, regression, and outlier detection that are effective in high-dimensional spaces and are memory efficient by using support vectors for decision making.
Support vector machine - Wikipedia - SVMs are max-margin supervised models that analyze data for classification and regression, using the kernel trick to enable efficient non-linear classification by mapping inputs to higher-dimensional feature spaces.
support vector machines (SVMs) - IBM - An SVM is a supervised algorithm that finds an optimal hyperplane maximizing the margin between classes and uses kernel functions to handle non-linearly separable data through the "kernel trick".
 dowidth.com
dowidth.com