Quantum-safe cryptography ensures data security against the potential threats posed by quantum computers, emphasizing resilience against quantum algorithms like Shor's. Lattice-based cryptography, a leading candidate within quantum-safe methods, leverages complex geometric structures to create hard mathematical problems resistant to quantum attacks. Explore the advancements and applications of these cutting-edge cryptographic techniques to understand the future of secure communications.
Why it is important
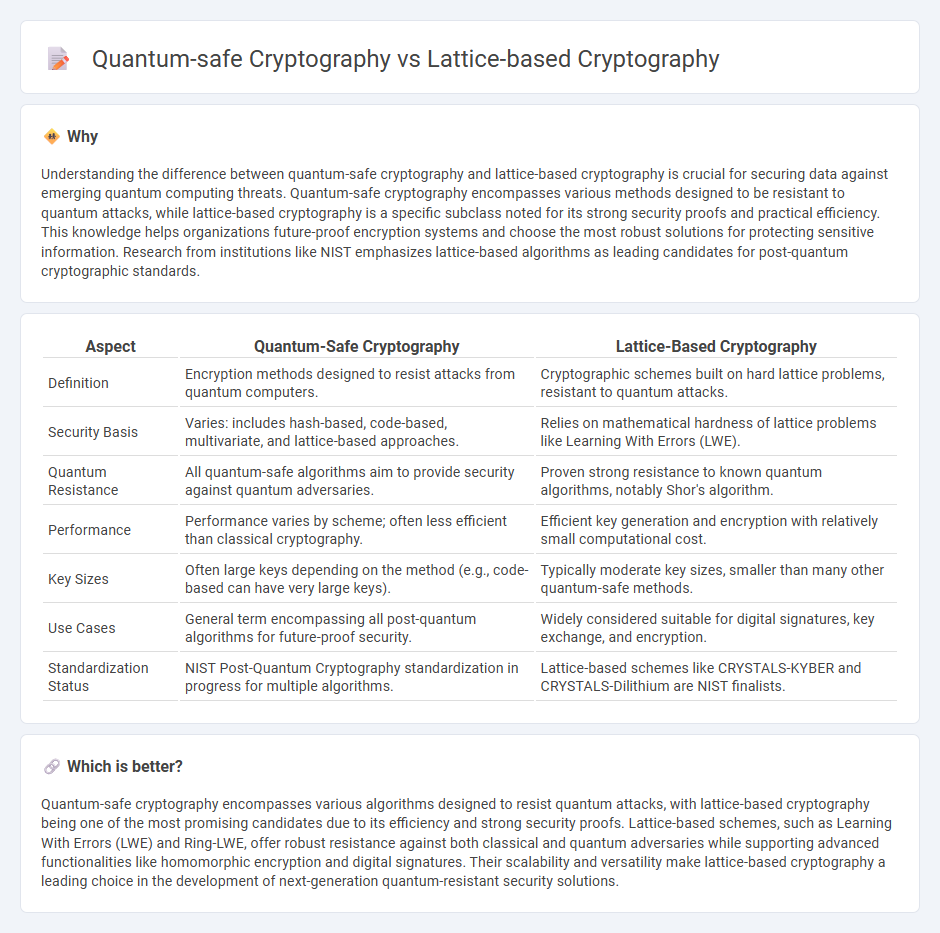
Understanding the difference between quantum-safe cryptography and lattice-based cryptography is crucial for securing data against emerging quantum computing threats. Quantum-safe cryptography encompasses various methods designed to be resistant to quantum attacks, while lattice-based cryptography is a specific subclass noted for its strong security proofs and practical efficiency. This knowledge helps organizations future-proof encryption systems and choose the most robust solutions for protecting sensitive information. Research from institutions like NIST emphasizes lattice-based algorithms as leading candidates for post-quantum cryptographic standards.
Comparison Table
| Aspect | Quantum-Safe Cryptography | Lattice-Based Cryptography |
|---|---|---|
| Definition | Encryption methods designed to resist attacks from quantum computers. | Cryptographic schemes built on hard lattice problems, resistant to quantum attacks. |
| Security Basis | Varies: includes hash-based, code-based, multivariate, and lattice-based approaches. | Relies on mathematical hardness of lattice problems like Learning With Errors (LWE). |
| Quantum Resistance | All quantum-safe algorithms aim to provide security against quantum adversaries. | Proven strong resistance to known quantum algorithms, notably Shor's algorithm. |
| Performance | Performance varies by scheme; often less efficient than classical cryptography. | Efficient key generation and encryption with relatively small computational cost. |
| Key Sizes | Often large keys depending on the method (e.g., code-based can have very large keys). | Typically moderate key sizes, smaller than many other quantum-safe methods. |
| Use Cases | General term encompassing all post-quantum algorithms for future-proof security. | Widely considered suitable for digital signatures, key exchange, and encryption. |
| Standardization Status | NIST Post-Quantum Cryptography standardization in progress for multiple algorithms. | Lattice-based schemes like CRYSTALS-KYBER and CRYSTALS-Dilithium are NIST finalists. |
Which is better?
Quantum-safe cryptography encompasses various algorithms designed to resist quantum attacks, with lattice-based cryptography being one of the most promising candidates due to its efficiency and strong security proofs. Lattice-based schemes, such as Learning With Errors (LWE) and Ring-LWE, offer robust resistance against both classical and quantum adversaries while supporting advanced functionalities like homomorphic encryption and digital signatures. Their scalability and versatility make lattice-based cryptography a leading choice in the development of next-generation quantum-resistant security solutions.
Connection
Quantum-safe cryptography ensures data security against quantum computer attacks by utilizing mathematical problems resistant to quantum algorithms, with lattice-based cryptography being one of the most promising approaches. Lattice-based cryptography relies on the hardness of lattice problems, such as the Learning With Errors (LWE) problem, which currently lack efficient quantum-solving methods. This connection places lattice-based cryptography at the forefront of developing secure, quantum-resistant cryptographic protocols essential for future-proof data protection.
Key Terms
Hard Lattice Problems
Hard lattice problems such as the Shortest Vector Problem (SVP) and Learning With Errors (LWE) form the foundation of lattice-based cryptography, offering robust resistance against quantum attacks. Quantum-safe cryptography encompasses various algorithms designed to secure data against quantum computers, with lattice-based schemes currently leading due to their balance of efficiency and security. Explore more about how these hard lattice problems ensure quantum resistance and their role in next-generation cryptographic standards.
Post-Quantum Security
Lattice-based cryptography offers robust security grounded in the hardness of problems like Learning With Errors (LWE), making it a prime candidate for post-quantum cryptographic algorithms resistant to quantum attacks. Quantum-safe cryptography encompasses a broad category of cryptographic methods designed to withstand quantum computing threats, with lattice-based schemes often leading due to their balance of security and efficiency. Explore the fundamental principles and comparative advantages of these approaches to understand the future landscape of post-quantum security.
NTRU
Lattice-based cryptography, exemplified by NTRU, leverages the hardness of lattice problems to offer strong security against quantum attacks, positioning it as a promising quantum-safe cryptographic solution. NTRU's efficient key generation, encryption, and decryption processes make it a practical choice for post-quantum cryptography standards. Explore the latest developments in NTRU and its role in securing communications against quantum threats.
Source and External Links
Post-quantum cryptography: Lattice-based cryptography - Lattice-based cryptography is a class of cryptographic systems built on hard mathematical problems in lattices, which are structures formed by combinations of vectors in multi-dimensional space, offering promising security against quantum attacks.
Lattice-based cryptography - It encompasses various cryptographic schemes, including encryption, key exchange (e.g., CRYSTALS-Kyber), homomorphic encryption, and hash functions, many of which are considered strong candidates for post-quantum standards.
Lattice based cryptography - This field has gained significant attention for its theoretical and practical potential, notably in constructing fully homomorphic encryption and providing security against advances in quantum computing.
 dowidth.com
dowidth.com