Post-quantum cryptography focuses on developing encryption methods resistant to quantum computer attacks, ensuring long-term data security. Isogeny-based cryptography, a subset of post-quantum techniques, leverages the mathematics of elliptic curve isogenies to create compact and efficient cryptographic schemes. Explore the differences and advancements in these cutting-edge technologies for secure communication in the quantum era.
Why it is important
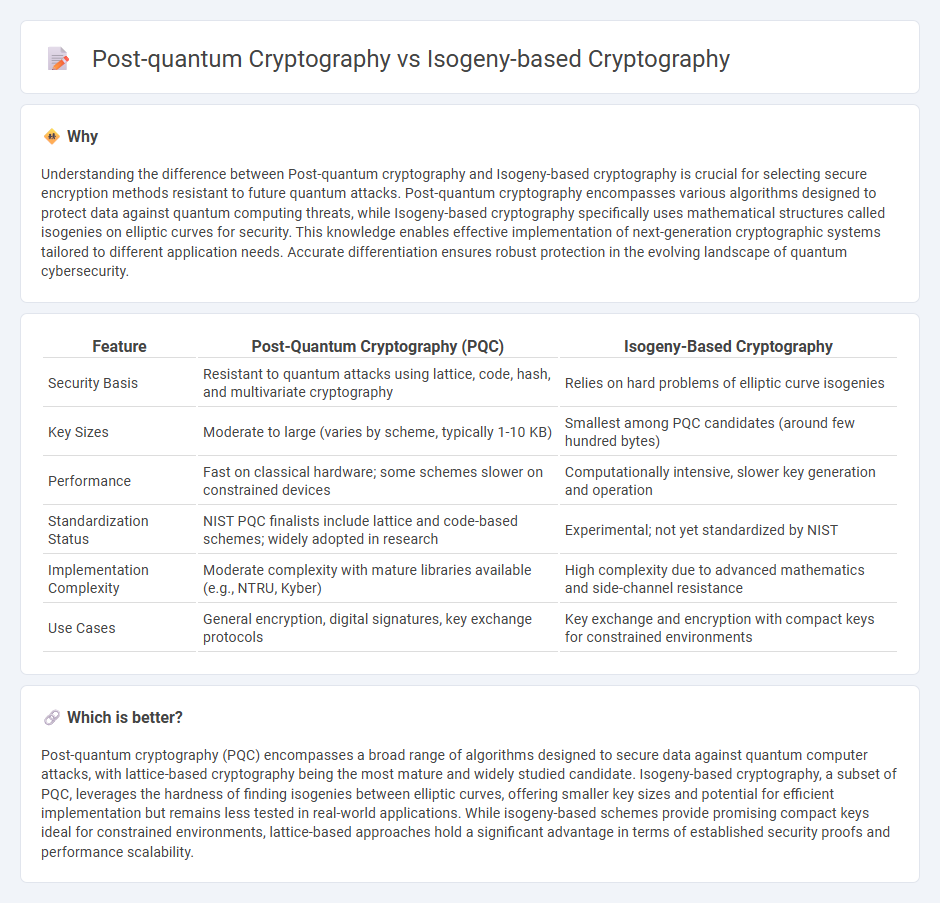
Understanding the difference between Post-quantum cryptography and Isogeny-based cryptography is crucial for selecting secure encryption methods resistant to future quantum attacks. Post-quantum cryptography encompasses various algorithms designed to protect data against quantum computing threats, while Isogeny-based cryptography specifically uses mathematical structures called isogenies on elliptic curves for security. This knowledge enables effective implementation of next-generation cryptographic systems tailored to different application needs. Accurate differentiation ensures robust protection in the evolving landscape of quantum cybersecurity.
Comparison Table
| Feature | Post-Quantum Cryptography (PQC) | Isogeny-Based Cryptography |
|---|---|---|
| Security Basis | Resistant to quantum attacks using lattice, code, hash, and multivariate cryptography | Relies on hard problems of elliptic curve isogenies |
| Key Sizes | Moderate to large (varies by scheme, typically 1-10 KB) | Smallest among PQC candidates (around few hundred bytes) |
| Performance | Fast on classical hardware; some schemes slower on constrained devices | Computationally intensive, slower key generation and operation |
| Standardization Status | NIST PQC finalists include lattice and code-based schemes; widely adopted in research | Experimental; not yet standardized by NIST |
| Implementation Complexity | Moderate complexity with mature libraries available (e.g., NTRU, Kyber) | High complexity due to advanced mathematics and side-channel resistance |
| Use Cases | General encryption, digital signatures, key exchange protocols | Key exchange and encryption with compact keys for constrained environments |
Which is better?
Post-quantum cryptography (PQC) encompasses a broad range of algorithms designed to secure data against quantum computer attacks, with lattice-based cryptography being the most mature and widely studied candidate. Isogeny-based cryptography, a subset of PQC, leverages the hardness of finding isogenies between elliptic curves, offering smaller key sizes and potential for efficient implementation but remains less tested in real-world applications. While isogeny-based schemes provide promising compact keys ideal for constrained environments, lattice-based approaches hold a significant advantage in terms of established security proofs and performance scalability.
Connection
Post-quantum cryptography addresses vulnerabilities in classical cryptographic systems posed by quantum computers, with isogeny-based cryptography emerging as a leading candidate due to its strong security assumptions rooted in the hardness of computing isogenies between elliptic curves. This approach leverages complex mathematical structures to enable secure key exchange and encryption resistant to quantum attacks, outperforming traditional methods vulnerable to Shor's algorithm. Ongoing research focuses on optimizing isogeny-based protocols for practical deployment in secure communications and blockchain technologies.
Key Terms
Supersingular Isogeny Diffie-Hellman (SIDH)
Supersingular Isogeny Diffie-Hellman (SIDH) is a pivotal scheme within post-quantum cryptography, leveraging the mathematical complexity of isogenies between supersingular elliptic curves to secure key exchanges against quantum attacks. Unlike lattice-based or code-based post-quantum methods, SIDH offers comparatively smaller key sizes and efficient transmission, making it attractive for constrained environments. Explore further to understand SIDH's role in advancing quantum-resistant cryptographic protocols.
Lattice-based cryptography
Isogeny-based cryptography leverages the mathematical structure of elliptic curve isogenies to create secure cryptographic schemes resistant to quantum attacks, while lattice-based cryptography relies on the hardness of lattice problems such as Learning With Errors (LWE) and Shortest Vector Problem (SVP) for post-quantum security. Lattice-based cryptography currently shows strong performance in terms of efficiency and scalability, making it a popular candidate in post-quantum cryptographic standardization efforts led by NIST. Explore the fundamental differences, security proofs, and practical implementations to better understand the strengths of each approach.
Quantum resistance
Isogeny-based cryptography leverages the hardness of finding isogenies between supersingular elliptic curves, offering strong resistance against attacks from quantum algorithms such as Shor's algorithm or Grover's algorithm, which threaten traditional cryptosystems. Compared to lattice-based and code-based post-quantum cryptographic schemes, isogeny-based protocols provide smaller key sizes and efficient key exchange mechanisms, maintaining security against both classical and quantum adversaries. Explore the latest research on isogeny-based cryptography to understand its evolving role in quantum-secure communication.
Source and External Links
Isogeny based cryptography - Isogeny-based cryptography is an elliptic-curve cryptography form relying on the difficulty of finding explicit isogenies between supersingular elliptic curves, and it currently remains resistant to known quantum attacks, unlike standard elliptic-curve cryptography.
Isogeny-Based Cryptography Tutorial - This tutorial introduces the mathematics behind supersingular isogeny-based cryptography and explains how it can provide quantum-safe key exchange protocols analogous to ECDH.
Supersingular isogeny key exchange - The SIDH protocol uses isogenies between supersingular elliptic curves over finite fields to establish shared secrets, offering a post-quantum key exchange method based on difficult isogeny problems.
 dowidth.com
dowidth.com