Differentiable programming integrates automatic differentiation into programming models, enabling optimization of complex functions often used in machine learning and scientific computing. Functional programming emphasizes pure functions, immutability, and higher-order functions to build reliable and maintainable software. Explore the distinct advantages and applications of differentiable and functional programming to understand their impact on modern software development.
Why it is important
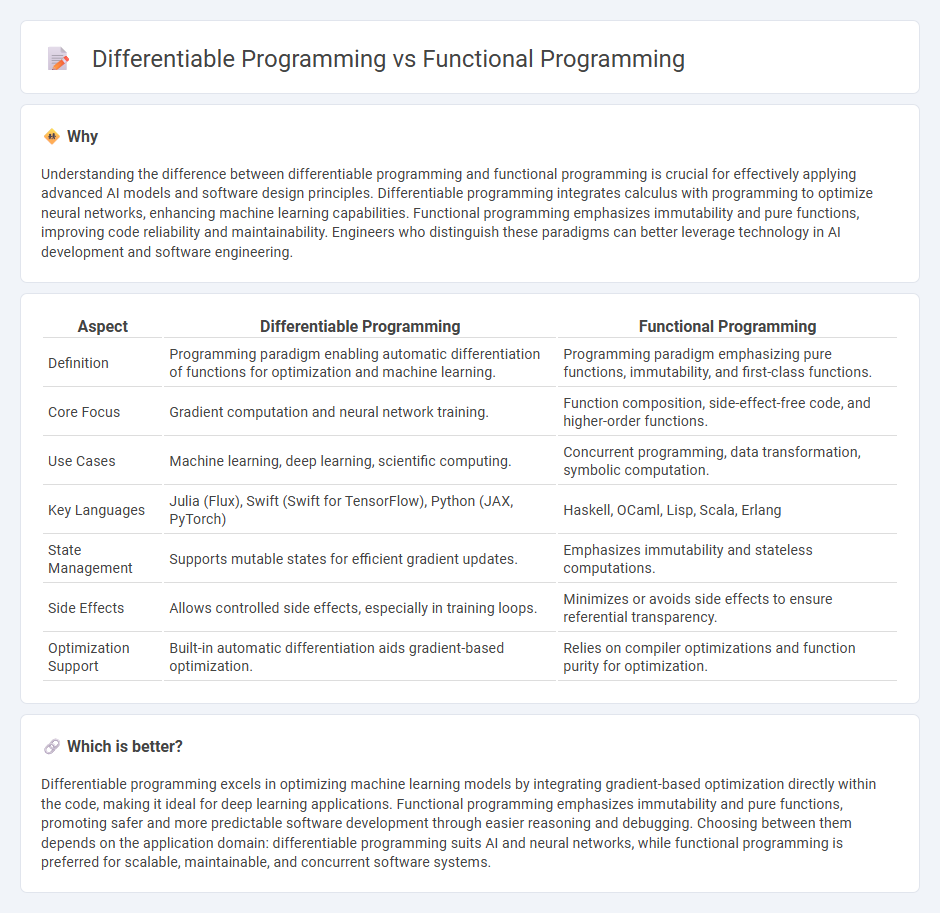
Understanding the difference between differentiable programming and functional programming is crucial for effectively applying advanced AI models and software design principles. Differentiable programming integrates calculus with programming to optimize neural networks, enhancing machine learning capabilities. Functional programming emphasizes immutability and pure functions, improving code reliability and maintainability. Engineers who distinguish these paradigms can better leverage technology in AI development and software engineering.
Comparison Table
| Aspect | Differentiable Programming | Functional Programming |
|---|---|---|
| Definition | Programming paradigm enabling automatic differentiation of functions for optimization and machine learning. | Programming paradigm emphasizing pure functions, immutability, and first-class functions. |
| Core Focus | Gradient computation and neural network training. | Function composition, side-effect-free code, and higher-order functions. |
| Use Cases | Machine learning, deep learning, scientific computing. | Concurrent programming, data transformation, symbolic computation. |
| Key Languages | Julia (Flux), Swift (Swift for TensorFlow), Python (JAX, PyTorch) | Haskell, OCaml, Lisp, Scala, Erlang |
| State Management | Supports mutable states for efficient gradient updates. | Emphasizes immutability and stateless computations. |
| Side Effects | Allows controlled side effects, especially in training loops. | Minimizes or avoids side effects to ensure referential transparency. |
| Optimization Support | Built-in automatic differentiation aids gradient-based optimization. | Relies on compiler optimizations and function purity for optimization. |
Which is better?
Differentiable programming excels in optimizing machine learning models by integrating gradient-based optimization directly within the code, making it ideal for deep learning applications. Functional programming emphasizes immutability and pure functions, promoting safer and more predictable software development through easier reasoning and debugging. Choosing between them depends on the application domain: differentiable programming suits AI and neural networks, while functional programming is preferred for scalable, maintainable, and concurrent software systems.
Connection
Differentiable programming leverages principles from functional programming by emphasizing pure functions and immutability, enabling efficient computation of derivatives through automatic differentiation. Functional programming's stateless design ensures compatibility with gradient-based optimization techniques central to differentiable programming. This connection facilitates the development of machine learning models by combining functional paradigms with differentiable computations.
Key Terms
**Immutability**
Immutability is a core principle in functional programming, ensuring that data structures cannot be altered after creation, which simplifies reasoning about code and enhances concurrency. In differentiable programming, while immutability supports clear gradient tracing and stable optimization, some frameworks allow mutable states to improve computational efficiency during backpropagation. To explore how immutability influences both paradigms in depth, delve into their respective impacts on program reliability and performance.
**Backpropagation**
Backpropagation is a fundamental algorithm in differentiable programming used to compute gradients efficiently for neural network training, leveraging calculus and chain rule properties. Functional programming emphasizes pure functions and immutability, facilitating clearer and more maintainable implementations of backpropagation by avoiding side effects. Explore deeper insights into how backpropagation integrates with these programming paradigms for optimized machine learning workflows.
**Pure Functions**
Pure functions in functional programming guarantee no side effects and consistent output for identical inputs, enabling easier reasoning and testing of code. Differentiable programming extends this paradigm by ensuring functions are smooth and differentiable, facilitating gradient-based optimization critical in machine learning models. Explore more to understand how pure functions influence model training and performance.
Source and External Links
What Is Functional Programming and Why Use It? - Functional programming (FP) uses pure functions, immutable data, and treats functions as first-class citizens to create maintainable, modular, and easy-to-debug software, focusing on declarations rather than execution statements and improving concurrency safety.
Introduction to Functional Programming - Functional programming is a declarative paradigm that uses pure functions, recursion instead of loops, immutability, first-class and higher-order functions to produce reliable and reusable code without side effects.
Functional Programming Paradigm - Functional programming is a declarative style focused on solving problems using pure mathematical functions and lambda calculus, emphasizing immutability, pure functions, and higher-order functions, and implemented in languages like Haskell, JavaScript, and Scala.
 dowidth.com
dowidth.com