Quantum key distribution (QKD) leverages the principles of quantum mechanics to ensure theoretically unbreakable encryption by securely sharing cryptographic keys. Elliptic curve cryptography (ECC) relies on the mathematical complexity of elliptic curves over finite fields to provide efficient and strong public-key encryption suitable for classical computing environments. Explore the strengths, vulnerabilities, and practical applications of QKD versus ECC to understand which technology leads in securing future communications.
Why it is important
Understanding the difference between quantum key distribution (QKD) and elliptic curve cryptography (ECC) is crucial for securing communications against future quantum computing threats. QKD uses principles of quantum mechanics to provide theoretically unbreakable encryption by detecting eavesdropping, whereas ECC relies on mathematical hardness assumptions that quantum computers could potentially compromise. This knowledge enables organizations to adopt appropriate encryption methods to protect sensitive data both now and in the post-quantum era. Selecting the right technology ensures long-term cybersecurity resilience and trust in digital communications.
Comparison Table
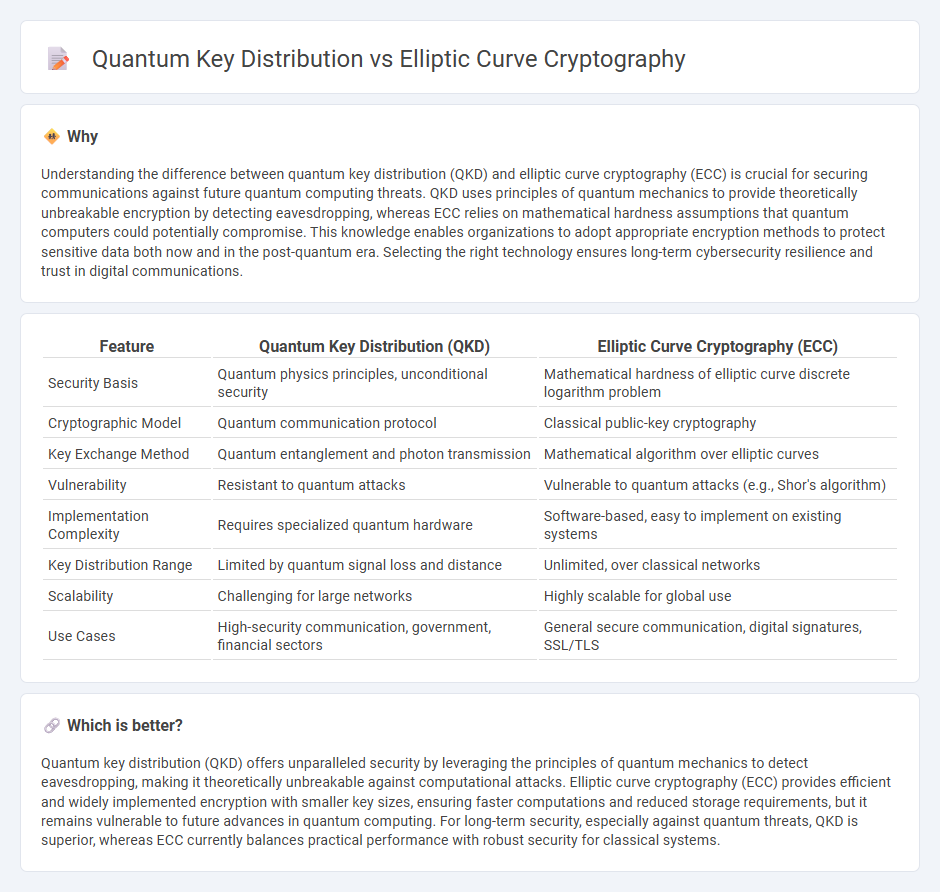
| Feature | Quantum Key Distribution (QKD) | Elliptic Curve Cryptography (ECC) |
|---|---|---|
| Security Basis | Quantum physics principles, unconditional security | Mathematical hardness of elliptic curve discrete logarithm problem |
| Cryptographic Model | Quantum communication protocol | Classical public-key cryptography |
| Key Exchange Method | Quantum entanglement and photon transmission | Mathematical algorithm over elliptic curves |
| Vulnerability | Resistant to quantum attacks | Vulnerable to quantum attacks (e.g., Shor's algorithm) |
| Implementation Complexity | Requires specialized quantum hardware | Software-based, easy to implement on existing systems |
| Key Distribution Range | Limited by quantum signal loss and distance | Unlimited, over classical networks |
| Scalability | Challenging for large networks | Highly scalable for global use |
| Use Cases | High-security communication, government, financial sectors | General secure communication, digital signatures, SSL/TLS |
Which is better?
Quantum key distribution (QKD) offers unparalleled security by leveraging the principles of quantum mechanics to detect eavesdropping, making it theoretically unbreakable against computational attacks. Elliptic curve cryptography (ECC) provides efficient and widely implemented encryption with smaller key sizes, ensuring faster computations and reduced storage requirements, but it remains vulnerable to future advances in quantum computing. For long-term security, especially against quantum threats, QKD is superior, whereas ECC currently balances practical performance with robust security for classical systems.
Connection
Quantum key distribution (QKD) and Elliptic Curve Cryptography (ECC) are both pivotal in advancing secure communication systems. QKD leverages the principles of quantum mechanics to enable theoretically unbreakable key exchange, while ECC provides efficient and robust cryptographic algorithms based on the mathematics of elliptic curves. Integration of QKD with ECC protocols enhances overall cybersecurity by combining quantum-resistant key distribution with computationally efficient encryption methods.
Key Terms
Public Key Infrastructure (PKI)
Elliptic curve cryptography (ECC) is widely implemented in Public Key Infrastructure (PKI) due to its strong security per key size and computational efficiency, making it suitable for digital certificates and secure communications. Quantum key distribution (QKD) offers theoretically unbreakable security by utilizing quantum mechanics to exchange encryption keys, but it requires specialized hardware and has limited integration with existing PKI systems. Explore further to understand how ECC and QKD complement or compete in evolving PKI landscapes.
Quantum Entanglement
Elliptic curve cryptography (ECC) relies on the mathematical hardness of the elliptic curve discrete logarithm problem, offering efficient and secure encryption used in current digital communications. Quantum key distribution (QKD) exploits quantum entanglement properties to enable theoretically unbreakable key exchange by detecting eavesdropping through the disturbance of entangled particle states. Explore the mechanisms and implications of quantum entanglement in cryptographic security to understand the future of secure communications.
Shor’s Algorithm
Elliptic curve cryptography (ECC) relies on the difficulty of solving discrete logarithm problems, making it vulnerable to Shor's Algorithm, which quantum computers can use to efficiently factor large integers and compute discrete logarithms. Quantum key distribution (QKD) leverages quantum mechanics principles to provide theoretically unbreakable encryption resistant to any computational attack, including those using Shor's Algorithm. Explore further to understand how emerging quantum technologies impact modern cryptographic methods.
Source and External Links
What is Elliptical Curve Cryptography (ECC)? - ECC is a public key encryption technique based on elliptic curve theory that enables faster, smaller, and more efficient cryptographic keys compared to traditional methods like RSA.
Elliptic-curve cryptography - ECC is a public-key cryptography approach using the algebraic structure of elliptic curves over finite fields, allowing equivalent security with much smaller keys than RSA or ElGamal.
What is elliptic curve cryptography? ECC for dummies - ECC is a public key cryptosystem where each user has a public-private key pair, with security relying on the mathematical properties of elliptic curves and the difficulty of solving the elliptic curve discrete logarithm problem.
 dowidth.com
dowidth.com