Post-quantum cryptography focuses on developing encryption algorithms resistant to attacks by quantum computers, ensuring data security in a future with advanced quantum capabilities. Code-based cryptography is a subset of post-quantum methods that relies on the hardness of decoding random linear codes, offering robust protection against quantum threats. Explore the latest advancements and practical applications in these cutting-edge cryptographic techniques to safeguard digital communications.
Why it is important
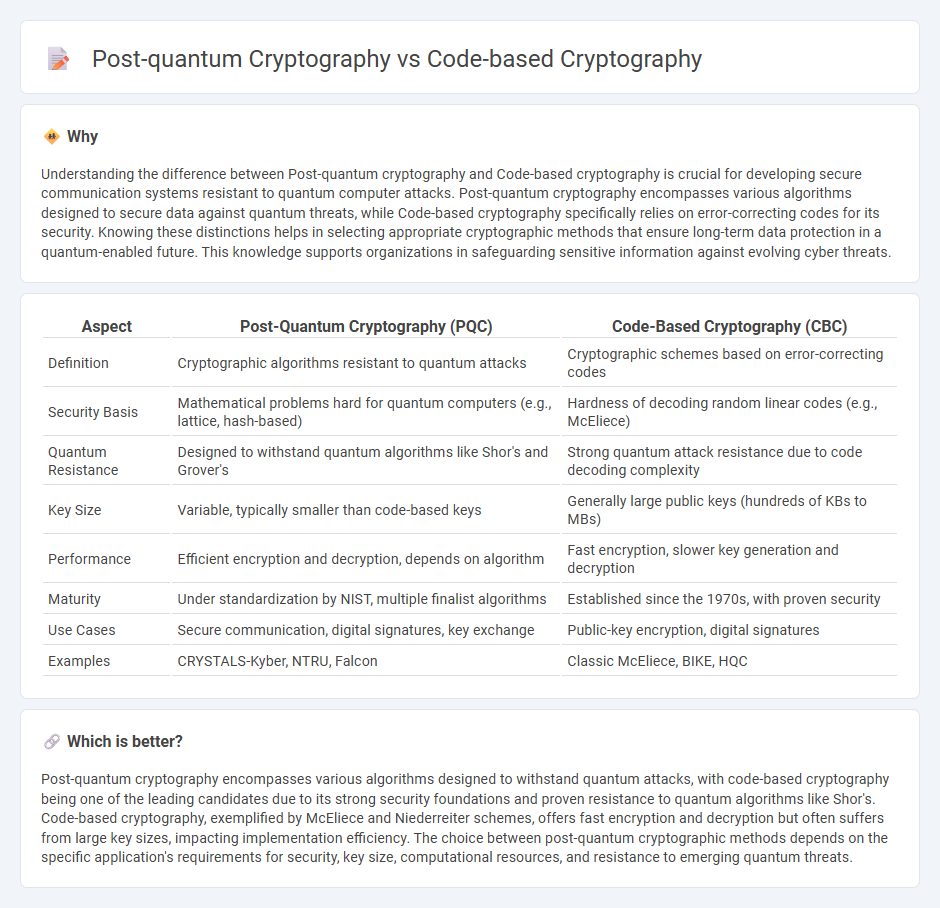
Understanding the difference between Post-quantum cryptography and Code-based cryptography is crucial for developing secure communication systems resistant to quantum computer attacks. Post-quantum cryptography encompasses various algorithms designed to secure data against quantum threats, while Code-based cryptography specifically relies on error-correcting codes for its security. Knowing these distinctions helps in selecting appropriate cryptographic methods that ensure long-term data protection in a quantum-enabled future. This knowledge supports organizations in safeguarding sensitive information against evolving cyber threats.
Comparison Table
| Aspect | Post-Quantum Cryptography (PQC) | Code-Based Cryptography (CBC) |
|---|---|---|
| Definition | Cryptographic algorithms resistant to quantum attacks | Cryptographic schemes based on error-correcting codes |
| Security Basis | Mathematical problems hard for quantum computers (e.g., lattice, hash-based) | Hardness of decoding random linear codes (e.g., McEliece) |
| Quantum Resistance | Designed to withstand quantum algorithms like Shor's and Grover's | Strong quantum attack resistance due to code decoding complexity |
| Key Size | Variable, typically smaller than code-based keys | Generally large public keys (hundreds of KBs to MBs) |
| Performance | Efficient encryption and decryption, depends on algorithm | Fast encryption, slower key generation and decryption |
| Maturity | Under standardization by NIST, multiple finalist algorithms | Established since the 1970s, with proven security |
| Use Cases | Secure communication, digital signatures, key exchange | Public-key encryption, digital signatures |
| Examples | CRYSTALS-Kyber, NTRU, Falcon | Classic McEliece, BIKE, HQC |
Which is better?
Post-quantum cryptography encompasses various algorithms designed to withstand quantum attacks, with code-based cryptography being one of the leading candidates due to its strong security foundations and proven resistance to quantum algorithms like Shor's. Code-based cryptography, exemplified by McEliece and Niederreiter schemes, offers fast encryption and decryption but often suffers from large key sizes, impacting implementation efficiency. The choice between post-quantum cryptographic methods depends on the specific application's requirements for security, key size, computational resources, and resistance to emerging quantum threats.
Connection
Post-quantum cryptography focuses on developing cryptographic algorithms resistant to quantum computer attacks, and code-based cryptography is a prominent candidate within this field due to its reliance on error-correcting codes for security. Code-based cryptographic schemes such as the McEliece cryptosystem offer strong resistance against quantum algorithms like Shor's algorithm, which threatens traditional RSA and ECC encryption. By leveraging the hardness of decoding random linear codes, code-based cryptography plays a critical role in securing data in a post-quantum era.
Key Terms
Lattice-based cryptography
Lattice-based cryptography, a core subset of post-quantum cryptography, leverages complex geometric structures to provide security against quantum attacks unlike traditional code-based cryptography, which relies on error-correcting codes like McEliece and Niederreiter schemes. The unique hardness assumptions related to lattice problems such as Learning With Errors (LWE) and Shortest Vector Problem (SVP) offer efficient encryption, digital signatures, and key exchange protocols resilient to both classical and quantum adversaries. Explore further to understand how lattice-based methods are driving the future of quantum-safe encryption standards.
Quantum resistance
Code-based cryptography leverages error-correcting codes to provide strong security against classical and quantum attacks, relying on the hardness of decoding random linear codes, making it a prominent candidate in post-quantum cryptography. Post-quantum cryptography encompasses various algorithms, including lattice-based, hash-based, and code-based schemes, all designed to resist quantum algorithms like Shor's and Grover's, with code-based cryptography specifically excelling in mitigating threats posed by quantum computing advancements. Explore further to understand the intricacies of quantum-resistant algorithms and their implementation in securing future communications.
Error-correcting codes
Code-based cryptography leverages error-correcting codes, such as McEliece and Niederreiter schemes, to create secure encryption methods resilient against quantum attacks by exploiting the hardness of decoding random linear codes. Post-quantum cryptography encompasses a broader range of algorithms designed to safeguard data from quantum computation threats, where code-based cryptosystems are prominent candidates due to their robust security assumptions and efficient implementations. Explore detailed insights on how error-correcting codes underpin the reliability and security of post-quantum cryptographic solutions.
Source and External Links
Code-based Cryptography - Utimaco - Code-based cryptography involves cryptographic systems secured by the difficulty of decoding linear error-correcting codes, such as Goppa codes.
CBCrypto - This is a platform for discussing code-based cryptography, which relies on hard coding-theoretic problems and is a candidate for post-quantum cryptography standards.
Survey on Code-based Cryptography - arXiv - This survey provides an extensive overview of code-based cryptography, including its mathematical background, security challenges, and ongoing research.
 dowidth.com
dowidth.com