Statistical arbitrage employs quantitative models to exploit pricing inefficiencies between related assets, using large datasets and machine learning for predictive accuracy. Mean reversion strategies focus on identifying price deviations from historical averages, anticipating a return to typical levels based on past patterns and volatility measures. Discover how these distinct trading approaches can enhance portfolio performance and risk management.
Why it is important
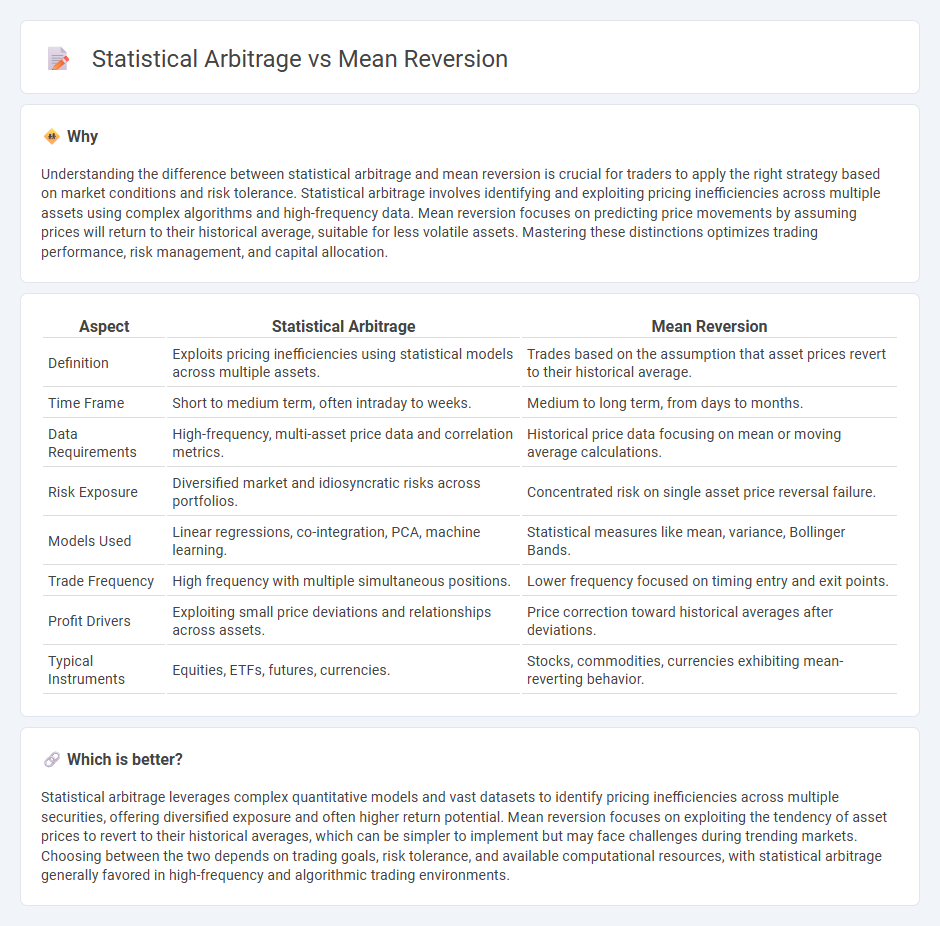
Understanding the difference between statistical arbitrage and mean reversion is crucial for traders to apply the right strategy based on market conditions and risk tolerance. Statistical arbitrage involves identifying and exploiting pricing inefficiencies across multiple assets using complex algorithms and high-frequency data. Mean reversion focuses on predicting price movements by assuming prices will return to their historical average, suitable for less volatile assets. Mastering these distinctions optimizes trading performance, risk management, and capital allocation.
Comparison Table
| Aspect | Statistical Arbitrage | Mean Reversion |
|---|---|---|
| Definition | Exploits pricing inefficiencies using statistical models across multiple assets. | Trades based on the assumption that asset prices revert to their historical average. |
| Time Frame | Short to medium term, often intraday to weeks. | Medium to long term, from days to months. |
| Data Requirements | High-frequency, multi-asset price data and correlation metrics. | Historical price data focusing on mean or moving average calculations. |
| Risk Exposure | Diversified market and idiosyncratic risks across portfolios. | Concentrated risk on single asset price reversal failure. |
| Models Used | Linear regressions, co-integration, PCA, machine learning. | Statistical measures like mean, variance, Bollinger Bands. |
| Trade Frequency | High frequency with multiple simultaneous positions. | Lower frequency focused on timing entry and exit points. |
| Profit Drivers | Exploiting small price deviations and relationships across assets. | Price correction toward historical averages after deviations. |
| Typical Instruments | Equities, ETFs, futures, currencies. | Stocks, commodities, currencies exhibiting mean-reverting behavior. |
Which is better?
Statistical arbitrage leverages complex quantitative models and vast datasets to identify pricing inefficiencies across multiple securities, offering diversified exposure and often higher return potential. Mean reversion focuses on exploiting the tendency of asset prices to revert to their historical averages, which can be simpler to implement but may face challenges during trending markets. Choosing between the two depends on trading goals, risk tolerance, and available computational resources, with statistical arbitrage generally favored in high-frequency and algorithmic trading environments.
Connection
Statistical arbitrage leverages mean reversion by identifying price discrepancies in correlated assets that tend to revert to their historical average. This trading strategy exploits short-term deviations from the mean, assuming prices will revert, enabling profitable buy and sell decisions. Algorithms analyze large datasets to detect these statistical patterns, optimizing trade execution and risk management in volatile markets.
Key Terms
Z-score
Mean reversion strategies involve identifying when asset prices deviate significantly from their historical average, often measured using the Z-score, which quantifies the number of standard deviations a data point is from the mean. Statistical arbitrage employs Z-scores to detect mispricings across related securities, allowing traders to exploit temporary price anomalies before they revert to their expected value. Explore the role of Z-score in refining risk management and enhancing return predictability in financial markets.
Cointegration
Mean reversion strategies exploit the tendency of asset prices to revert to their historical averages, relying heavily on statistical measures like cointegration to identify pairs or groups of assets with stable long-term relationships. Statistical arbitrage leverages cointegration by constructing portfolios that capitalize on temporary deviations from equilibrium, aiming to profit as prices revert to a mean determined by their joint behavior rather than individual trends. Explore deeper concepts of cointegration in trading models to enhance strategy robustness and profitability.
Pairs Trading
Pairs trading leverages mean reversion by identifying two historically correlated assets whose price relationship diverges temporarily, allowing traders to profit when prices revert to the mean. Statistical arbitrage expands this concept using quantitative models and vast datasets to exploit pricing inefficiencies across multiple securities, enhancing risk-adjusted returns. Discover how advanced algorithms and real-time data analysis refine pairs trading strategies for more effective market opportunities.
Source and External Links
Mean Reversion Strategies: Introduction, Trading, Strategies and More - Mean reversion is a financial theory suggesting that asset prices and historical returns eventually revert to their long-term mean, with trading strategies involving identifying the mean, detecting deviations, generating buy/sell signals, and executing trades accordingly.
Mean reversion (finance) - Wikipedia - Mean reversion assumes asset prices tend to converge to an average price over time, guiding timing strategies by identifying trading ranges and averages to predict price corrections after deviations.
Mean Reversion - Overview, Trading, Impact of Catalysts - Mean reversion theory implies asset prices move towards a long-term mean, with trading strategies exploiting deviations by buying undervalued (below mean) assets and selling overvalued (above mean) ones, often influenced by market catalysts.
 dowidth.com
dowidth.com