Homomorphic encryption allows computations on encrypted data without revealing the underlying information, enabling secure cloud processing and privacy-preserving analytics. Zero-knowledge proofs enable one party to prove knowledge of specific information to another party without disclosing the information itself, enhancing secure authentication and blockchain applications. Explore the detailed differences and practical uses of homomorphic encryption and zero-knowledge proofs to understand their impact on modern cybersecurity.
Why it is important
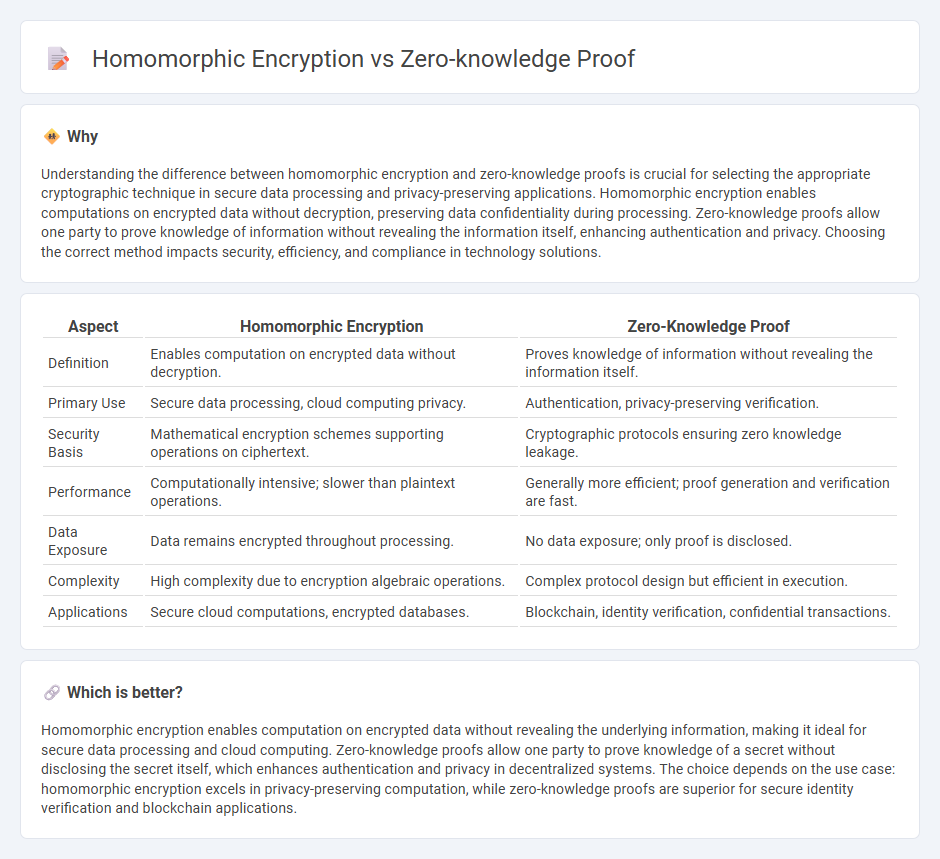
Understanding the difference between homomorphic encryption and zero-knowledge proofs is crucial for selecting the appropriate cryptographic technique in secure data processing and privacy-preserving applications. Homomorphic encryption enables computations on encrypted data without decryption, preserving data confidentiality during processing. Zero-knowledge proofs allow one party to prove knowledge of information without revealing the information itself, enhancing authentication and privacy. Choosing the correct method impacts security, efficiency, and compliance in technology solutions.
Comparison Table
| Aspect | Homomorphic Encryption | Zero-Knowledge Proof |
|---|---|---|
| Definition | Enables computation on encrypted data without decryption. | Proves knowledge of information without revealing the information itself. |
| Primary Use | Secure data processing, cloud computing privacy. | Authentication, privacy-preserving verification. |
| Security Basis | Mathematical encryption schemes supporting operations on ciphertext. | Cryptographic protocols ensuring zero knowledge leakage. |
| Performance | Computationally intensive; slower than plaintext operations. | Generally more efficient; proof generation and verification are fast. |
| Data Exposure | Data remains encrypted throughout processing. | No data exposure; only proof is disclosed. |
| Complexity | High complexity due to encryption algebraic operations. | Complex protocol design but efficient in execution. |
| Applications | Secure cloud computations, encrypted databases. | Blockchain, identity verification, confidential transactions. |
Which is better?
Homomorphic encryption enables computation on encrypted data without revealing the underlying information, making it ideal for secure data processing and cloud computing. Zero-knowledge proofs allow one party to prove knowledge of a secret without disclosing the secret itself, which enhances authentication and privacy in decentralized systems. The choice depends on the use case: homomorphic encryption excels in privacy-preserving computation, while zero-knowledge proofs are superior for secure identity verification and blockchain applications.
Connection
Homomorphic encryption and zero-knowledge proof are connected through their role in enhancing data privacy and security within cryptographic systems. Homomorphic encryption allows computations to be performed on encrypted data without decryption, preserving confidentiality, while zero-knowledge proofs enable one party to prove knowledge of information without revealing the information itself. Together, they enable secure, privacy-preserving computations and verifications in applications like blockchain, secure voting, and confidential transactions.
Key Terms
Privacy
Zero-knowledge proof allows one party to prove knowledge of information without revealing the information itself, maintaining strong privacy guarantees during verification processes. Homomorphic encryption enables computations on encrypted data without decrypting it, ensuring data privacy while allowing data processing in untrusted environments. Explore how these cryptographic methods protect privacy in various applications.
Computation
Zero-knowledge proofs enable a prover to demonstrate knowledge of a secret without revealing the secret itself, optimizing verification without exposing sensitive data during computation. Homomorphic encryption allows computations to be performed directly on encrypted data, ensuring data privacy while processing. Explore deeper into the computational advantages and applications of both cryptographic techniques.
Verification
Zero-knowledge proof enables one party to verify the truth of a statement without revealing any additional information, ensuring privacy during the verification process. Homomorphic encryption allows computations on encrypted data, guaranteeing that verification can be performed without decrypting sensitive information. Explore deeper insights on zero-knowledge proof and homomorphic encryption to enhance secure verification methodologies.
Source and External Links
Zero-Knowledge Proof (ZKP) -- Explained - Zero-knowledge proofs allow one party (the prover) to prove to another (the verifier) that a statement about some data is true without revealing the data itself, satisfying completeness, soundness, and zero-knowledge properties, often illustrated by the cave-door example where knowledge of a secret passcode is proven without revealing it.
Zero-knowledge proof - A zero-knowledge proof is a protocol where a prover convinces a verifier that a statement is true without revealing any information beyond the truth of the statement, fulfilling completeness, soundness, and zero-knowledge conditions, and is probabilistic rather than deterministic in nature.
Zero Knowledge Proofs: An illustrated primer, Part 2 - Zero-knowledge proofs involve an interaction where a prover convinces a verifier that a mathematical statement is true without revealing any additional information, requiring the properties of completeness, soundness, and zero-knowledge.
 dowidth.com
dowidth.com