Quantum-safe cryptography aims to protect data against the potential threats posed by quantum computers, with isogeny-based cryptography emerging as a promising approach by leveraging mathematical structures from elliptic curve theory. Isogeny-based protocols offer compact key sizes and strong security assumptions compared to other quantum-resistant algorithms like lattice-based cryptography. Explore the intricate mechanisms and benefits of these quantum-safe techniques to better understand the future of secure communication.
Why it is important
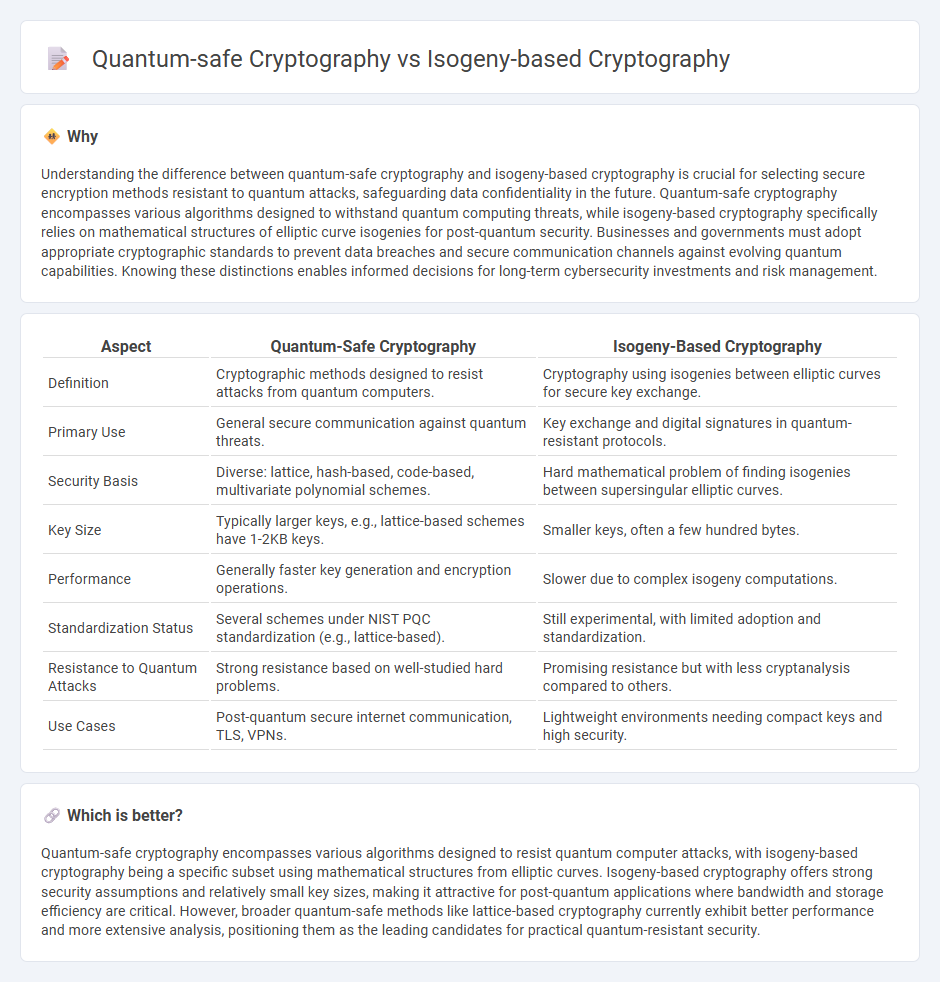
Understanding the difference between quantum-safe cryptography and isogeny-based cryptography is crucial for selecting secure encryption methods resistant to quantum attacks, safeguarding data confidentiality in the future. Quantum-safe cryptography encompasses various algorithms designed to withstand quantum computing threats, while isogeny-based cryptography specifically relies on mathematical structures of elliptic curve isogenies for post-quantum security. Businesses and governments must adopt appropriate cryptographic standards to prevent data breaches and secure communication channels against evolving quantum capabilities. Knowing these distinctions enables informed decisions for long-term cybersecurity investments and risk management.
Comparison Table
| Aspect | Quantum-Safe Cryptography | Isogeny-Based Cryptography |
|---|---|---|
| Definition | Cryptographic methods designed to resist attacks from quantum computers. | Cryptography using isogenies between elliptic curves for secure key exchange. |
| Primary Use | General secure communication against quantum threats. | Key exchange and digital signatures in quantum-resistant protocols. |
| Security Basis | Diverse: lattice, hash-based, code-based, multivariate polynomial schemes. | Hard mathematical problem of finding isogenies between supersingular elliptic curves. |
| Key Size | Typically larger keys, e.g., lattice-based schemes have 1-2KB keys. | Smaller keys, often a few hundred bytes. |
| Performance | Generally faster key generation and encryption operations. | Slower due to complex isogeny computations. |
| Standardization Status | Several schemes under NIST PQC standardization (e.g., lattice-based). | Still experimental, with limited adoption and standardization. |
| Resistance to Quantum Attacks | Strong resistance based on well-studied hard problems. | Promising resistance but with less cryptanalysis compared to others. |
| Use Cases | Post-quantum secure internet communication, TLS, VPNs. | Lightweight environments needing compact keys and high security. |
Which is better?
Quantum-safe cryptography encompasses various algorithms designed to resist quantum computer attacks, with isogeny-based cryptography being a specific subset using mathematical structures from elliptic curves. Isogeny-based cryptography offers strong security assumptions and relatively small key sizes, making it attractive for post-quantum applications where bandwidth and storage efficiency are critical. However, broader quantum-safe methods like lattice-based cryptography currently exhibit better performance and more extensive analysis, positioning them as the leading candidates for practical quantum-resistant security.
Connection
Quantum-safe cryptography aims to secure communication against quantum computer threats by using mathematical problems resistant to quantum attacks, with Isogeny-based cryptography being a prime example leveraging hardness of computing isogenies between elliptic curves. The connection lies in Isogeny-based cryptography's potential to provide compact keys and efficient protocols suitable for post-quantum security standards. This approach addresses vulnerabilities in traditional cryptographic systems, ensuring confidentiality and integrity in a quantum computing era.
Key Terms
Supersingular Isogeny
Supersingular isogeny-based cryptography leverages the mathematical structure of supersingular elliptic curves to create secure key exchange protocols resistant to quantum attacks, unlike classical schemes vulnerable to Shor's algorithm. This approach offers smaller key sizes and efficient performance compared to other quantum-safe methods like lattice-based or hash-based cryptography, making it a promising candidate for practical post-quantum security. Explore the unique properties and real-world applications of supersingular isogeny cryptography to understand its role in the future of quantum-safe encryption.
Lattice-based Cryptography
Lattice-based cryptography stands out in quantum-safe cryptography for its strong resistance to quantum attacks and efficient key generation, encryption, and decryption processes. Unlike isogeny-based cryptography, which relies on the hardness of finding isogenies between elliptic curves, lattice-based schemes leverage the complexity of lattice problems such as Learning With Errors (LWE) and Shortest Vector Problem (SVP) for security. Explore the advantages, applications, and challenges of lattice-based cryptography to understand its critical role in securing future communications against quantum threats.
Post-Quantum Security
Isogeny-based cryptography leverages complex mathematical structures of elliptic curves to create secure keys resistant to quantum attacks, offering a promising approach within post-quantum security paradigms. Compared to other quantum-safe cryptographic methods like lattice-based or code-based cryptography, isogeny-based schemes often have smaller key sizes and higher efficiency in key exchange processes. Explore the intricate mechanisms and practical applications of isogeny-based cryptography to understand its role in advancing quantum-safe security solutions.
Source and External Links
Isogeny based cryptography - Gaurish Korpal - Isogeny-based cryptography is a form of elliptic-curve cryptography whose security depends on the difficulty of finding explicit isogenies between supersingular elliptic curves, and it is currently considered quantum-safe unlike standard ECC which is vulnerable to quantum attacks.
Isogeny-Based Cryptography Tutorial - ISARA Corporation - This tutorial introduces the mathematics behind supersingular isogeny-based cryptography and describes key establishment protocols analogous to ECDH that offer promising quantum-resistant security alternatives.
Supersingular isogeny key exchange - Wikipedia - Supersingular Isogeny Diffie-Hellman (SIDH) is a post-quantum key exchange protocol based on secret isogenies between supersingular elliptic curves, allowing two parties to establish a shared secret securely, though recent research has found weaknesses in some variants.
 dowidth.com
dowidth.com