Liquid neural networks leverage continuous-time dynamics to process complex temporal data, enabling adaptive learning and robust decision-making in fluctuating environments. Hyperdimensional computing employs high-dimensional vectors to represent data, facilitating efficient, noise-resistant computations inspired by cognitive processes. Explore these cutting-edge technologies to understand their distinct advantages and applications in modern AI systems.
Why it is important
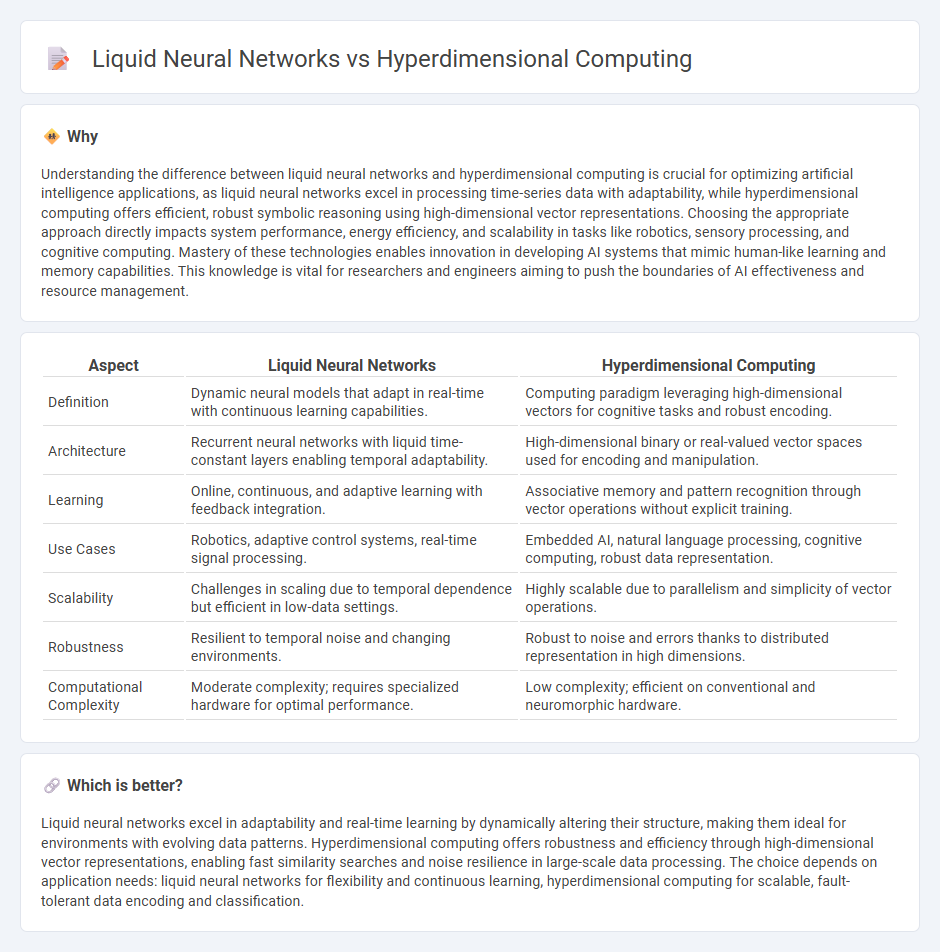
Understanding the difference between liquid neural networks and hyperdimensional computing is crucial for optimizing artificial intelligence applications, as liquid neural networks excel in processing time-series data with adaptability, while hyperdimensional computing offers efficient, robust symbolic reasoning using high-dimensional vector representations. Choosing the appropriate approach directly impacts system performance, energy efficiency, and scalability in tasks like robotics, sensory processing, and cognitive computing. Mastery of these technologies enables innovation in developing AI systems that mimic human-like learning and memory capabilities. This knowledge is vital for researchers and engineers aiming to push the boundaries of AI effectiveness and resource management.
Comparison Table
| Aspect | Liquid Neural Networks | Hyperdimensional Computing |
|---|---|---|
| Definition | Dynamic neural models that adapt in real-time with continuous learning capabilities. | Computing paradigm leveraging high-dimensional vectors for cognitive tasks and robust encoding. |
| Architecture | Recurrent neural networks with liquid time-constant layers enabling temporal adaptability. | High-dimensional binary or real-valued vector spaces used for encoding and manipulation. |
| Learning | Online, continuous, and adaptive learning with feedback integration. | Associative memory and pattern recognition through vector operations without explicit training. |
| Use Cases | Robotics, adaptive control systems, real-time signal processing. | Embedded AI, natural language processing, cognitive computing, robust data representation. |
| Scalability | Challenges in scaling due to temporal dependence but efficient in low-data settings. | Highly scalable due to parallelism and simplicity of vector operations. |
| Robustness | Resilient to temporal noise and changing environments. | Robust to noise and errors thanks to distributed representation in high dimensions. |
| Computational Complexity | Moderate complexity; requires specialized hardware for optimal performance. | Low complexity; efficient on conventional and neuromorphic hardware. |
Which is better?
Liquid neural networks excel in adaptability and real-time learning by dynamically altering their structure, making them ideal for environments with evolving data patterns. Hyperdimensional computing offers robustness and efficiency through high-dimensional vector representations, enabling fast similarity searches and noise resilience in large-scale data processing. The choice depends on application needs: liquid neural networks for flexibility and continuous learning, hyperdimensional computing for scalable, fault-tolerant data encoding and classification.
Connection
Liquid neural networks leverage continuous-time dynamics and adaptive structures to process information similarly to hyperdimensional computing, which represents data in high-dimensional vectors that enable robust and efficient pattern recognition. Both paradigms emphasize flexibility and fault tolerance, allowing systems to handle noisy, uncertain, or incomplete data by mimicking brain-like computational principles. This connection underpins advances in AI robustness, enabling more adaptive and scalable models in robotics, autonomic control, and real-time decision-making tasks.
Key Terms
High-dimensional vectors
High-dimensional vectors in hyperdimensional computing enable robust representations using thousands of dimensions for efficient pattern recognition and memory storage. Liquid neural networks leverage dynamic, continuous-time processing but typically operate with lower-dimensional embeddings compared to hyperdimensional vectors. Discover how these differing approaches impact scalability and adaptability in advanced machine learning systems.
Dynamic temporal processing
Hyperdimensional computing leverages high-dimensional vectors to represent and manipulate temporal sequences through robust, distributed encoding, enabling efficient pattern recognition over time. Liquid neural networks dynamically adjust internal states in continuous time, providing exceptional adaptability for temporal data and complex, time-varying inputs. Explore deeper insights into their mechanisms and performance in dynamic temporal processing to enhance your understanding.
State-space representation
Hyperdimensional computing employs high-dimensional vectors to represent state-space, enabling robust and distributed information encoding that is inherently noise-tolerant and scalable. Liquid neural networks utilize continuous-time state-space models with dynamic, adaptable states that evolve according to differential equations, offering real-time learning and flexibility in temporal dynamics. Explore how these differing state-space representations impact applications in cognitive computing and adaptive systems.
Source and External Links
Hyperdimensional computing - Hyperdimensional computing (HDC) is a computational approach modeling information as high-dimensional vectors (hypervectors), inspired by brain function, enabling robust and noise-tolerant learning and memory representations especially for artificial general intelligence applications.
A New Approach to Computation Reimagines Artificial Intelligence - HDC uses very high-dimensional vectors with nearly orthogonal random components to efficiently represent and manipulate symbolic information, allowing fast, transparent, and robust AI computations.
Collection of Hyperdimensional Computing Projects - HDC operates on hypervectors--high-dimensional random vectors--that support simple arithmetic operations such as addition and multiplication, and offer scalable, memory-centric, and noise-robust computing architectures with applications in fast learning without backpropagation.
 dowidth.com
dowidth.com