Quantum advantage demonstrates the practical superiority of quantum computers in solving specific problems faster than classical counterparts, with Shor's algorithm exemplifying this by efficiently factoring large integers, a task that underpins modern cryptographic security. Shor's algorithm leverages quantum parallelism to break widely used encryption methods, signaling a transformative impact on cybersecurity and computational complexity. Explore the intricacies of quantum advantage and Shor's algorithm to understand their revolutionary implications in technology.
Why it is important
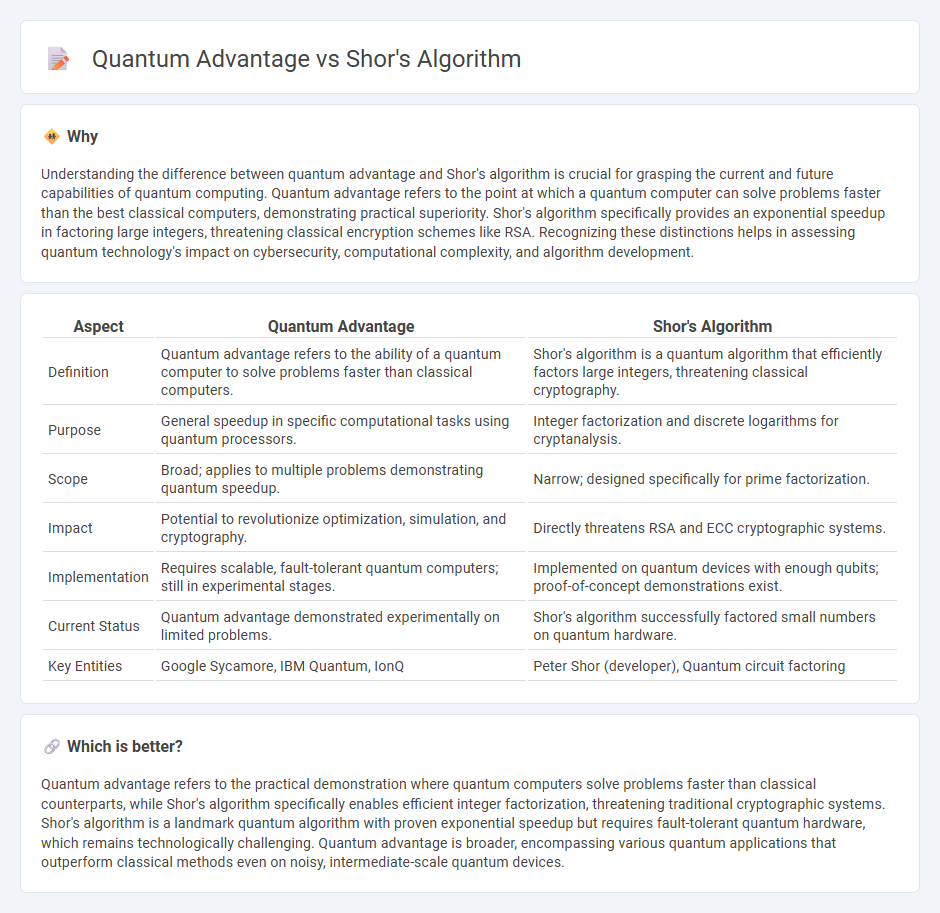
Understanding the difference between quantum advantage and Shor's algorithm is crucial for grasping the current and future capabilities of quantum computing. Quantum advantage refers to the point at which a quantum computer can solve problems faster than the best classical computers, demonstrating practical superiority. Shor's algorithm specifically provides an exponential speedup in factoring large integers, threatening classical encryption schemes like RSA. Recognizing these distinctions helps in assessing quantum technology's impact on cybersecurity, computational complexity, and algorithm development.
Comparison Table
| Aspect | Quantum Advantage | Shor's Algorithm |
|---|---|---|
| Definition | Quantum advantage refers to the ability of a quantum computer to solve problems faster than classical computers. | Shor's algorithm is a quantum algorithm that efficiently factors large integers, threatening classical cryptography. |
| Purpose | General speedup in specific computational tasks using quantum processors. | Integer factorization and discrete logarithms for cryptanalysis. |
| Scope | Broad; applies to multiple problems demonstrating quantum speedup. | Narrow; designed specifically for prime factorization. |
| Impact | Potential to revolutionize optimization, simulation, and cryptography. | Directly threatens RSA and ECC cryptographic systems. |
| Implementation | Requires scalable, fault-tolerant quantum computers; still in experimental stages. | Implemented on quantum devices with enough qubits; proof-of-concept demonstrations exist. |
| Current Status | Quantum advantage demonstrated experimentally on limited problems. | Shor's algorithm successfully factored small numbers on quantum hardware. |
| Key Entities | Google Sycamore, IBM Quantum, IonQ | Peter Shor (developer), Quantum circuit factoring |
Which is better?
Quantum advantage refers to the practical demonstration where quantum computers solve problems faster than classical counterparts, while Shor's algorithm specifically enables efficient integer factorization, threatening traditional cryptographic systems. Shor's algorithm is a landmark quantum algorithm with proven exponential speedup but requires fault-tolerant quantum hardware, which remains technologically challenging. Quantum advantage is broader, encompassing various quantum applications that outperform classical methods even on noisy, intermediate-scale quantum devices.
Connection
Quantum advantage is demonstrated when quantum computers solve problems faster than classical counterparts, with Shor's algorithm providing a prime example by efficiently factoring large integers. This algorithm exploits quantum superposition and entanglement to reduce the complexity of integer factorization from sub-exponential to polynomial time. The impact of Shor's algorithm on cryptography highlights the significant potential of quantum advantage in transforming computational security frameworks.
Key Terms
Quantum Speedup
Shor's algorithm demonstrates a significant quantum speedup by efficiently factoring large integers exponentially faster than the best-known classical algorithms, which is crucial for cryptography and cybersecurity. This quantum speedup exemplifies a clear quantum advantage by solving problems infeasible for classical computers within practical timeframes. Explore how Shor's algorithm propels the frontier of quantum computing performance and its implications for future technologies.
Integer Factorization
Shor's algorithm offers exponential speedup for integer factorization compared to classical algorithms by utilizing quantum Fourier transform and periodicity detection. This breakthrough is pivotal in demonstrating quantum advantage, challenging RSA cryptosystems based on factorization hardness. Explore further to understand how Shor's algorithm shapes the future of cryptography and quantum computing.
Classical Computational Limits
Shor's algorithm demonstrates a quantum advantage by efficiently factoring large integers, a task believed to be computationally infeasible for classical algorithms due to the exponential time complexity of classical factoring methods like the general number field sieve. Classical computational limits are highlighted by the inability of classical systems to solve integer factorization problems within polynomial time, contrasting with Shor's polynomial-time performance on quantum computers. Explore further to understand the implications of Shor's algorithm on classical cryptographic security and quantum computational breakthroughs.
Source and External Links
Shor's algorithm - Wikipedia - Shor's algorithm is a quantum algorithm developed by Peter Shor in 1994 for efficiently finding the prime factors of an integer, running in polynomial time on a quantum computer, which is exponentially faster than the best known classical algorithms.
What is Shor's Algorithm - QuEra Computing - Shor's Algorithm uses the Quantum Fourier Transform and Quantum Phase Estimation to find the period of a function related to the number to be factored, enabling efficient prime factorization on a quantum computer.
Quantum Cryptography - Shor's Algorithm Explained - Classiq - Shor's algorithm starts with classical steps and uses a quantum computer to find the period of a number, helping to factorize large integers much faster than classical methods, fundamentally impacting cryptography.
 dowidth.com
dowidth.com