Diffusion models and normalizing flows are advanced generative techniques used in machine learning for data synthesis and representation. Diffusion models iteratively transform noise into structured data through stochastic processes, while normalizing flows apply invertible transformations to map complex distributions to simpler ones. Explore the differences and applications of these models to understand their impact on AI advancements.
Why it is important
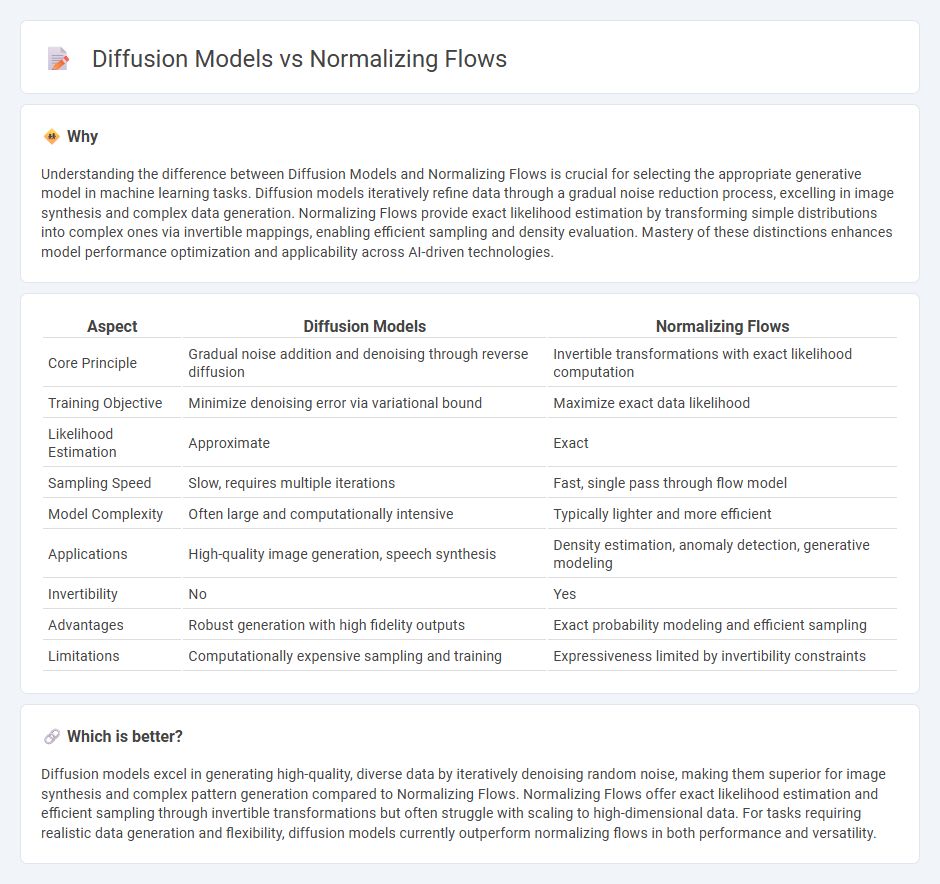
Understanding the difference between Diffusion Models and Normalizing Flows is crucial for selecting the appropriate generative model in machine learning tasks. Diffusion models iteratively refine data through a gradual noise reduction process, excelling in image synthesis and complex data generation. Normalizing Flows provide exact likelihood estimation by transforming simple distributions into complex ones via invertible mappings, enabling efficient sampling and density evaluation. Mastery of these distinctions enhances model performance optimization and applicability across AI-driven technologies.
Comparison Table
| Aspect | Diffusion Models | Normalizing Flows |
|---|---|---|
| Core Principle | Gradual noise addition and denoising through reverse diffusion | Invertible transformations with exact likelihood computation |
| Training Objective | Minimize denoising error via variational bound | Maximize exact data likelihood |
| Likelihood Estimation | Approximate | Exact |
| Sampling Speed | Slow, requires multiple iterations | Fast, single pass through flow model |
| Model Complexity | Often large and computationally intensive | Typically lighter and more efficient |
| Applications | High-quality image generation, speech synthesis | Density estimation, anomaly detection, generative modeling |
| Invertibility | No | Yes |
| Advantages | Robust generation with high fidelity outputs | Exact probability modeling and efficient sampling |
| Limitations | Computationally expensive sampling and training | Expressiveness limited by invertibility constraints |
Which is better?
Diffusion models excel in generating high-quality, diverse data by iteratively denoising random noise, making them superior for image synthesis and complex pattern generation compared to Normalizing Flows. Normalizing Flows offer exact likelihood estimation and efficient sampling through invertible transformations but often struggle with scaling to high-dimensional data. For tasks requiring realistic data generation and flexibility, diffusion models currently outperform normalizing flows in both performance and versatility.
Connection
Diffusion models and Normalizing Flows both leverage probabilistic frameworks to transform complex data distributions into simpler ones, facilitating efficient sampling and density estimation. Diffusion models progressively add noise to data and learn to reverse this process, while Normalizing Flows apply a sequence of invertible mappings to achieve exact likelihood computation. Their connection lies in the shared goal of modeling data generation through continuous transformations governed by deep neural networks.
Key Terms
Latent Variable Modeling
Normalizing Flows excel in latent variable modeling by providing exact likelihood computation through invertible transformations, enabling efficient sampling and density estimation. Diffusion models rely on iterative denoising processes, progressively refining latent representations to approximate complex data distributions with high fidelity. Explore these methodologies further to understand their distinct advantages in generative modeling frameworks.
Probability Density Estimation
Normalizing Flows provide exact probability density estimation through invertible transformations with tractable Jacobians, allowing efficient sampling and likelihood evaluation. Diffusion models approximate complex distributions by gradually denoising data through stochastic processes, typically achieving high-quality sample generation but less straightforward exact density computation. Explore deeper insights and comparative advantages of Normalizing Flows and Diffusion models in probabilistic modeling.
Generative Training Dynamics
Normalizing flows employ invertible transformations to map complex data distributions into simple latent spaces, optimizing likelihood directly and enabling exact density estimation during generative training. Diffusion models gradually transform noise into data through a stochastic denoising process, relying on score matching to model the underlying data distribution with high fidelity. Explore deeper insights into their generative training dynamics and performance differences to enhance your understanding of advanced generative modeling techniques.
Source and External Links
Normalizing Flows Explained - Papers With Code - Normalizing Flows construct complex probability distributions by applying a series of invertible and smooth transformations on an initial simple density, enabling the explicit computation of the transformed density using the change of variables formula and Jacobian determinants.
Normalizing Flow Models - Normalizing flow models use deterministic, invertible mappings preserving dimensionality, allowing both tractable likelihood computation and feature learning by composing invertible functions with efficiently computable Jacobian determinants.
Flow-based generative model - Wikipedia - A flow-based generative model explicitly models probability distributions through normalizing flows, applying invertible transformations such as normalized linear flows and using Jacobian determinant to maintain density normalization.
 dowidth.com
dowidth.com