Neural Radiance Fields (NeRF) leverage deep learning to generate photorealistic 3D scenes by modeling volumetric radiance and density, while Signed Distance Fields (SDF) represent surfaces implicitly through the shortest distance to the nearest boundary, enabling efficient shape reconstruction and rendering. NeRF excels in capturing complex lighting and view-dependent effects, whereas SDFs provide precise geometric control and facilitate operations like collision detection and mesh extraction. Explore the latest advancements in NeRF and SDF technologies to transform 3D modeling and visualization workflows.
Why it is important
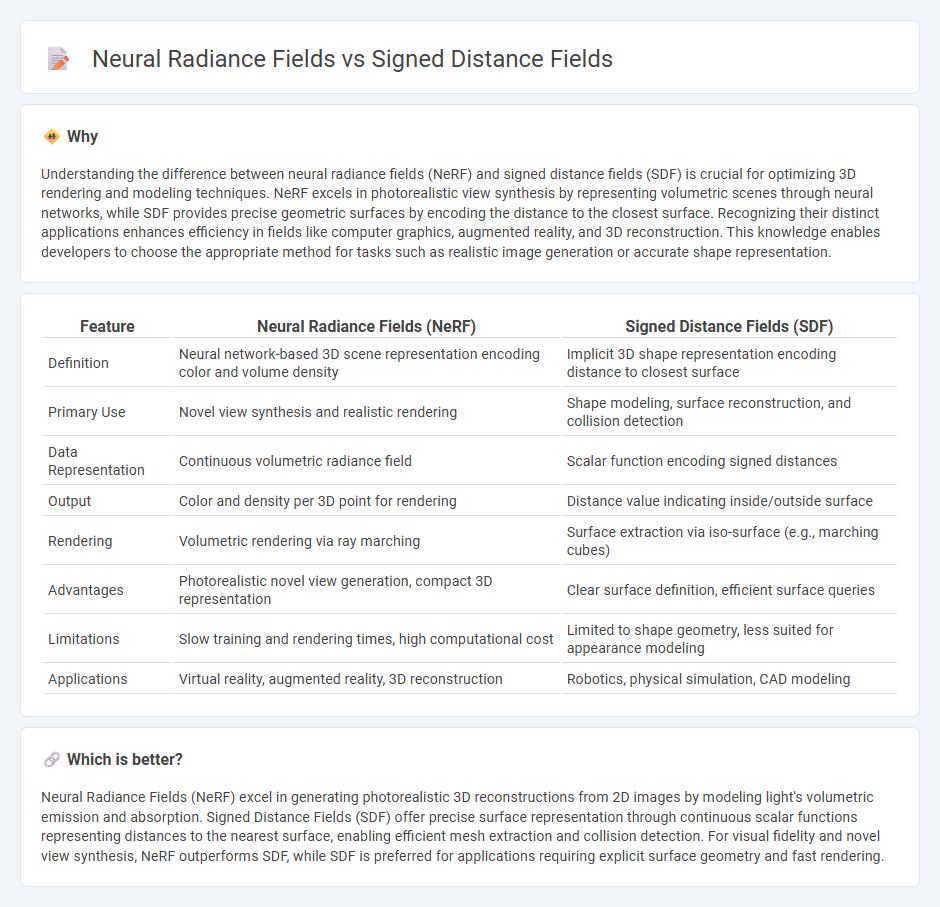
Understanding the difference between neural radiance fields (NeRF) and signed distance fields (SDF) is crucial for optimizing 3D rendering and modeling techniques. NeRF excels in photorealistic view synthesis by representing volumetric scenes through neural networks, while SDF provides precise geometric surfaces by encoding the distance to the closest surface. Recognizing their distinct applications enhances efficiency in fields like computer graphics, augmented reality, and 3D reconstruction. This knowledge enables developers to choose the appropriate method for tasks such as realistic image generation or accurate shape representation.
Comparison Table
| Feature | Neural Radiance Fields (NeRF) | Signed Distance Fields (SDF) |
|---|---|---|
| Definition | Neural network-based 3D scene representation encoding color and volume density | Implicit 3D shape representation encoding distance to closest surface |
| Primary Use | Novel view synthesis and realistic rendering | Shape modeling, surface reconstruction, and collision detection |
| Data Representation | Continuous volumetric radiance field | Scalar function encoding signed distances |
| Output | Color and density per 3D point for rendering | Distance value indicating inside/outside surface |
| Rendering | Volumetric rendering via ray marching | Surface extraction via iso-surface (e.g., marching cubes) |
| Advantages | Photorealistic novel view generation, compact 3D representation | Clear surface definition, efficient surface queries |
| Limitations | Slow training and rendering times, high computational cost | Limited to shape geometry, less suited for appearance modeling |
| Applications | Virtual reality, augmented reality, 3D reconstruction | Robotics, physical simulation, CAD modeling |
Which is better?
Neural Radiance Fields (NeRF) excel in generating photorealistic 3D reconstructions from 2D images by modeling light's volumetric emission and absorption. Signed Distance Fields (SDF) offer precise surface representation through continuous scalar functions representing distances to the nearest surface, enabling efficient mesh extraction and collision detection. For visual fidelity and novel view synthesis, NeRF outperforms SDF, while SDF is preferred for applications requiring explicit surface geometry and fast rendering.
Connection
Neural Radiance Fields (NeRFs) and Signed Distance Fields (SDFs) are connected through their shared use in 3D scene representation and reconstruction, leveraging neural networks to model spatial information. NeRFs focus on volumetric rendering by predicting color and density at any spatial coordinate, while SDFs encode the geometry of surfaces by representing the signed distance to the closest surface boundary. Integrating SDFs with NeRFs enhances scene understanding by combining precise geometric boundaries with photorealistic rendering, enabling more accurate and detailed 3D reconstructions.
Key Terms
Implicit Representation
Signed distance fields (SDFs) represent implicit surfaces by encoding the shortest distance to the object boundary, enabling efficient geometric queries and smooth surface reconstructions. Neural radiance fields (NeRFs) implicitly model volumetric scene appearance by learning view-dependent color and density functions through deep neural networks, allowing photorealistic rendering from sparse input views. Explore the nuances and applications of implicit representations in 3D vision to deepen your understanding of these transformative technologies.
Rendering
Signed distance fields (SDFs) provide efficient rendering by encoding surfaces as zero-level sets, allowing for fast ray-marching and geometric queries in real-time applications. Neural radiance fields (NeRFs) excel at photorealistic view synthesis by modeling volumetric scene representation with learned radiance and density, but often require computationally intensive neural network evaluations for rendering. Explore deeper comparisons to understand their trade-offs in rendering quality, speed, and application domains.
Scene Reconstruction
Signed distance fields (SDFs) represent 3D geometry by encoding the shortest distance from any point in space to the object's surface, enabling efficient and precise scene reconstruction with smooth surface representation and easy mesh extraction. Neural radiance fields (NeRFs) model scenes through volumetric volumetric radiance, capturing complex light interactions and photorealistic rendering by estimating color and density along rays, but often require higher computational resources and struggle with explicit geometry extraction. Explore further to understand how these complementary approaches balance accuracy and rendering fidelity in 3D scene reconstruction.
Source and External Links
Signed distance function - A signed distance field (SDF) is a function that gives the orthogonal distance from any point to the boundary of a shape, with the sign indicating whether the point is inside or outside the shape, typically positive inside and negative outside or vice versa.
Ray Marching and Signed Distance Fields - SDFs enable efficient GPU ray-marching techniques where a ray is advanced by the distance given by the SDF, allowing fast rendering of complex shapes like spheres, cubes, and toruses by computing minimum distances to surfaces.
Intro to Signed Distance Fields - SDFs can be understood visually by mapping each pixel's coordinate to a distance value representing the closest edge of a shape, facilitating rendering and combining of complex geometries in 2D or 3D.
 dowidth.com
dowidth.com