Homomorphic encryption enables computations on encrypted data without revealing the underlying information, offering secure data processing in cloud environments. Lattice-based cryptography relies on the hardness of lattice problems, providing strong resistance against quantum attacks and forming the basis for post-quantum cryptographic solutions. Explore the distinctions and applications of these advanced encryption methods to understand their impact on future cybersecurity.
Why it is important
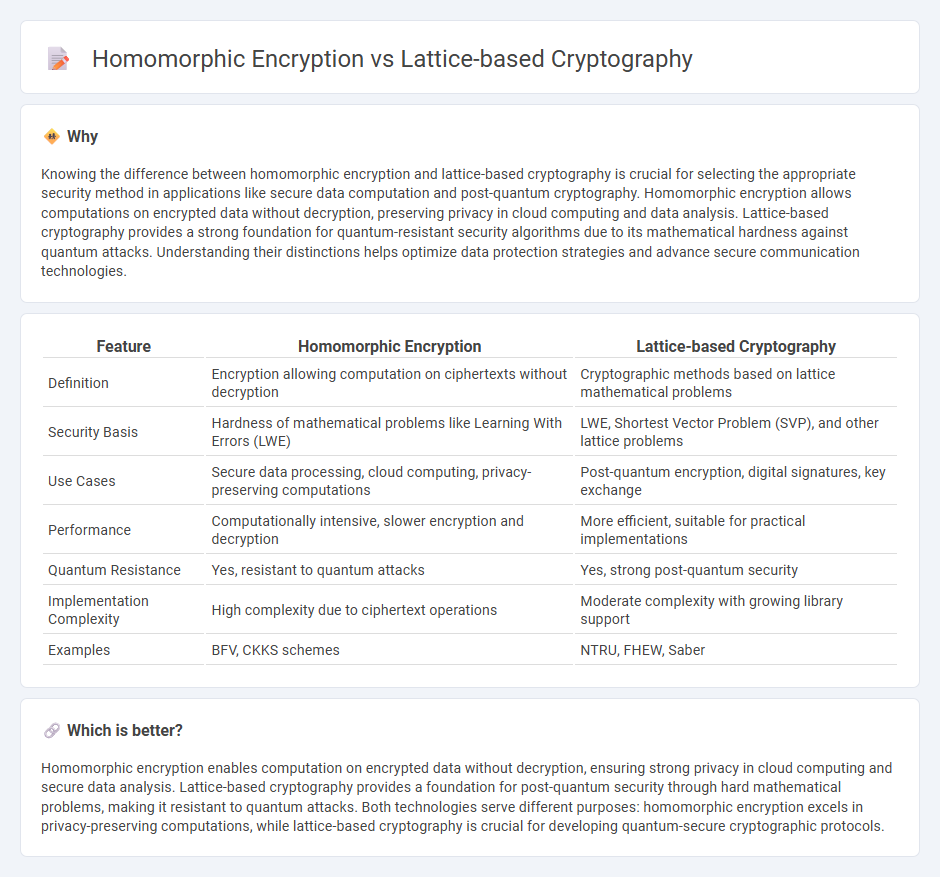
Knowing the difference between homomorphic encryption and lattice-based cryptography is crucial for selecting the appropriate security method in applications like secure data computation and post-quantum cryptography. Homomorphic encryption allows computations on encrypted data without decryption, preserving privacy in cloud computing and data analysis. Lattice-based cryptography provides a strong foundation for quantum-resistant security algorithms due to its mathematical hardness against quantum attacks. Understanding their distinctions helps optimize data protection strategies and advance secure communication technologies.
Comparison Table
| Feature | Homomorphic Encryption | Lattice-based Cryptography |
|---|---|---|
| Definition | Encryption allowing computation on ciphertexts without decryption | Cryptographic methods based on lattice mathematical problems |
| Security Basis | Hardness of mathematical problems like Learning With Errors (LWE) | LWE, Shortest Vector Problem (SVP), and other lattice problems |
| Use Cases | Secure data processing, cloud computing, privacy-preserving computations | Post-quantum encryption, digital signatures, key exchange |
| Performance | Computationally intensive, slower encryption and decryption | More efficient, suitable for practical implementations |
| Quantum Resistance | Yes, resistant to quantum attacks | Yes, strong post-quantum security |
| Implementation Complexity | High complexity due to ciphertext operations | Moderate complexity with growing library support |
| Examples | BFV, CKKS schemes | NTRU, FHEW, Saber |
Which is better?
Homomorphic encryption enables computation on encrypted data without decryption, ensuring strong privacy in cloud computing and secure data analysis. Lattice-based cryptography provides a foundation for post-quantum security through hard mathematical problems, making it resistant to quantum attacks. Both technologies serve different purposes: homomorphic encryption excels in privacy-preserving computations, while lattice-based cryptography is crucial for developing quantum-secure cryptographic protocols.
Connection
Homomorphic encryption relies on lattice-based cryptography to enable secure computation on encrypted data without decryption, leveraging the mathematical hardness of lattice problems for strong cryptographic security. Lattice-based cryptographic schemes provide the foundational structures that support the complex operations required in homomorphic encryption algorithms. These connections enhance data privacy and security in applications like cloud computing and secure multiparty computation.
Key Terms
Trapdoor Functions (Lattice-based Cryptography)
Lattice-based cryptography relies on the hardness of lattice problems like the Shortest Vector Problem (SVP) and Learning With Errors (LWE), with trapdoor functions enabling secure key generation and efficient decryption. These trapdoor functions create a one-way mapping that is easy to compute but infeasible to invert without a secret trapdoor, forming the foundation for cryptographic schemes resilient against quantum attacks. Explore in-depth how trapdoor functions empower secure lattice-based protocols and compare their role with homomorphic encryption mechanisms.
Fully Homomorphic Encryption (Homomorphic Encryption)
Fully Homomorphic Encryption (FHE) enables computation on encrypted data without decryption, relying heavily on lattice-based cryptography for its security foundation, which is resistant to quantum attacks. Lattice structures provide the mathematical hardness that underpins FHE schemes, allowing complex operations such as addition and multiplication to be securely executed on ciphertexts. Explore the latest advancements and practical applications of FHE in secure data processing for enhanced privacy protection.
Learning With Errors (LWE)
Lattice-based cryptography, particularly through the Learning With Errors (LWE) problem, provides strong security grounded in the hardness of solving noisy linear equations over lattices, making it resistant to quantum attacks. Homomorphic encryption enables computation directly on encrypted data without decryption, with LWE-based schemes offering practical efficiency and security in this domain. Explore more about how LWE underpins advanced cryptographic protocols for secure, private computations.
Source and External Links
Post-quantum cryptography: Lattice-based cryptography - Red Hat - Lattice-based cryptography is a class of cryptographic systems based on hard mathematical problems involving lattices, which are sets of vectors formed by linear combinations that create multidimensional grids used for securing data against quantum attacks.
Prepping for post-quantum: a beginner's guide to lattice cryptography - Lattice-based cryptography is the primary candidate to replace elliptic curve cryptography in the post-quantum era due to its security against quantum attacks and comparable speed, though it requires significantly more data communication, which poses engineering challenges.
Lattice-based cryptography - Wikipedia - It encompasses various cryptographic schemes such as NTRUEncrypt and CRYSTALS-Kyber for encryption and key exchange, relying on problems like learning with errors (LWE), and has been adopted for post-quantum standards due to its resilience against quantum computing threats.
 dowidth.com
dowidth.com