Post-quantum cryptography is designed to secure data against the capabilities of quantum computers, which can break traditional cryptographic algorithms such as Elliptic Curve Cryptography (ECC). ECC relies on the difficulty of mathematical problems like the elliptic curve discrete logarithm, but quantum algorithms like Shor's algorithm threaten its security. Explore how post-quantum cryptography is shaping the future of secure communication by learning more about its advancements and applications.
Why it is important
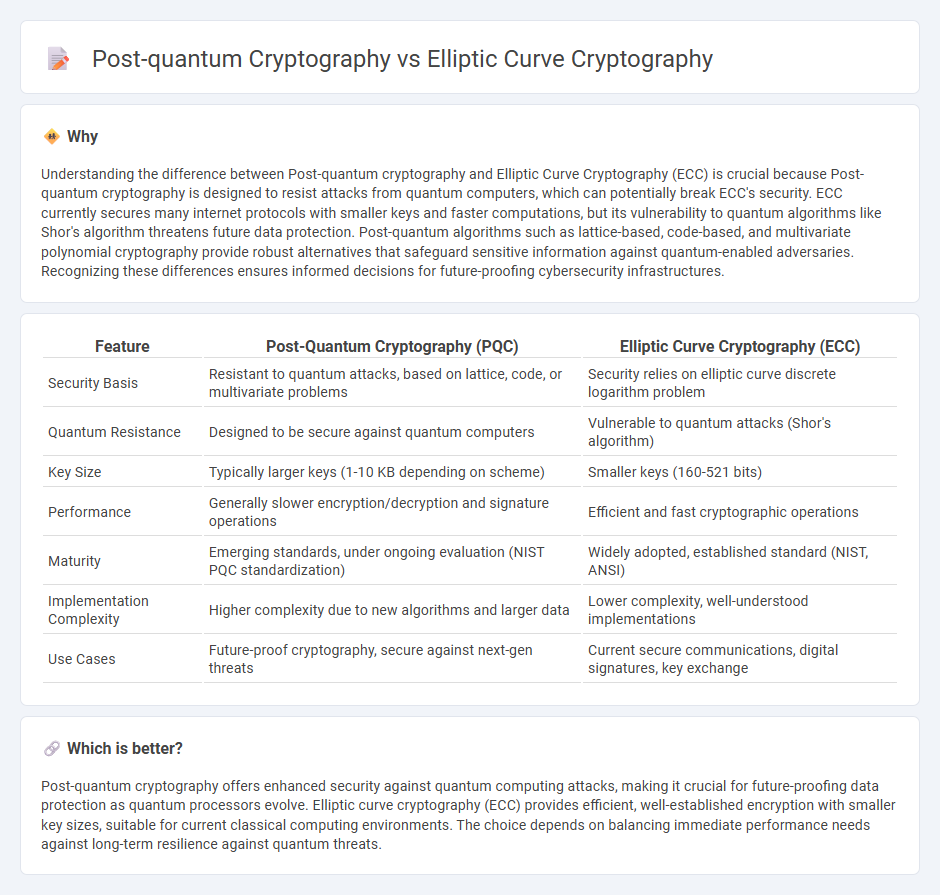
Understanding the difference between Post-quantum cryptography and Elliptic Curve Cryptography (ECC) is crucial because Post-quantum cryptography is designed to resist attacks from quantum computers, which can potentially break ECC's security. ECC currently secures many internet protocols with smaller keys and faster computations, but its vulnerability to quantum algorithms like Shor's algorithm threatens future data protection. Post-quantum algorithms such as lattice-based, code-based, and multivariate polynomial cryptography provide robust alternatives that safeguard sensitive information against quantum-enabled adversaries. Recognizing these differences ensures informed decisions for future-proofing cybersecurity infrastructures.
Comparison Table
| Feature | Post-Quantum Cryptography (PQC) | Elliptic Curve Cryptography (ECC) |
|---|---|---|
| Security Basis | Resistant to quantum attacks, based on lattice, code, or multivariate problems | Security relies on elliptic curve discrete logarithm problem |
| Quantum Resistance | Designed to be secure against quantum computers | Vulnerable to quantum attacks (Shor's algorithm) |
| Key Size | Typically larger keys (1-10 KB depending on scheme) | Smaller keys (160-521 bits) |
| Performance | Generally slower encryption/decryption and signature operations | Efficient and fast cryptographic operations |
| Maturity | Emerging standards, under ongoing evaluation (NIST PQC standardization) | Widely adopted, established standard (NIST, ANSI) |
| Implementation Complexity | Higher complexity due to new algorithms and larger data | Lower complexity, well-understood implementations |
| Use Cases | Future-proof cryptography, secure against next-gen threats | Current secure communications, digital signatures, key exchange |
Which is better?
Post-quantum cryptography offers enhanced security against quantum computing attacks, making it crucial for future-proofing data protection as quantum processors evolve. Elliptic curve cryptography (ECC) provides efficient, well-established encryption with smaller key sizes, suitable for current classical computing environments. The choice depends on balancing immediate performance needs against long-term resilience against quantum threats.
Connection
Post-quantum cryptography and Elliptic Curve Cryptography (ECC) both focus on securing digital communications, but post-quantum cryptography aims to protect against the computational power of quantum computers that can break ECC's underlying mathematical problems. While ECC relies on the hardness of the elliptic curve discrete logarithm problem, post-quantum algorithms utilize lattice-based, hash-based, or code-based structures resilient to quantum attacks. The transition from ECC to post-quantum cryptography represents a critical evolution in cryptographic standards to maintain digital security in the quantum era.
Key Terms
Discrete Logarithm Problem (ECC)
Elliptic Curve Cryptography (ECC) relies on the hardness of the Discrete Logarithm Problem (DLP) over elliptic curves, offering efficient key sizes and strong security under classical computational assumptions. Post-Quantum Cryptography (PQC) aims to develop cryptographic systems resilient against quantum attacks, which threaten ECC by efficiently solving DLP via Shor's algorithm. Explore the advancements and challenges in transitioning from ECC to PQC to secure digital communication against emerging quantum threats.
Quantum Resistance (Post-quantum)
Elliptic curve cryptography (ECC) relies on the hardness of the discrete logarithm problem, which quantum computers can solve efficiently using Shor's algorithm, rendering ECC vulnerable to future quantum attacks. Post-quantum cryptography (PQC) employs algorithms based on lattice problems, hash-based signatures, and code-based cryptography that are currently believed to resist quantum decryption methods. Explore the latest advancements in cryptographic standards to understand the evolving landscape of quantum-resistant security solutions.
Lattice-based Cryptography (Post-quantum)
Elliptic Curve Cryptography (ECC) relies on the hardness of the elliptic curve discrete logarithm problem, providing efficient and secure encryption with smaller key sizes but faces vulnerabilities against quantum algorithms like Shor's algorithm. Post-quantum cryptography, particularly lattice-based cryptography, leverages the complexity of lattice problems such as Learning With Errors (LWE) and Ring-LWE, offering quantum-resistant security that can protect data against future quantum computer attacks. Explore further to understand how lattice-based cryptographic schemes are shaping the next generation of secure communication protocols.
Source and External Links
What is Elliptical Curve Cryptography (ECC)? - TechTarget - ECC is a public key encryption technique based on elliptic curve theory that creates faster, smaller, and more efficient cryptographic keys, used as an alternative to RSA for tasks like digital signatures in cryptocurrencies and email encryption.
Elliptic-curve cryptography - Wikipedia - ECC is a public-key cryptography approach based on elliptic curves over finite fields, enabling smaller keys to provide equivalent security as RSA and commonly used for key agreement, digital signatures, and encryption.
What is Elliptic Curve Cryptography (ECC)? - SSL.com - ECC uses the mathematical properties of elliptic curves where a private key multiplies a generator point to produce a public key, and its security depends on the difficulty of the Elliptic Curve Discrete Logarithm Problem (ECDLP).
 dowidth.com
dowidth.com