Diffusion models generate high-quality data by simulating gradual noise reduction processes, excelling in image synthesis and representation learning. Energy-Based Models (EBMs) define data likelihood through energy functions, focusing on capturing complex data distributions and enabling flexible, interpretable model structures. Explore the nuances and applications of both approaches to understand their impact on advancing artificial intelligence technologies.
Why it is important
Understanding the difference between Diffusion Models and Energy-Based Models is crucial for advancing AI research, as Diffusion Models excel in generating high-quality data through iterative noise reduction, while Energy-Based Models focus on learning complex data distributions using energy functions. Diffusion Models have achieved state-of-the-art results in image synthesis, making them essential for applications in computer vision and generative tasks. Energy-Based Models provide a flexible framework for unsupervised learning and anomaly detection by modeling the probability density of data. Mastering these differences enables researchers and practitioners to choose the most effective approach for specific machine learning problems.
Comparison Table
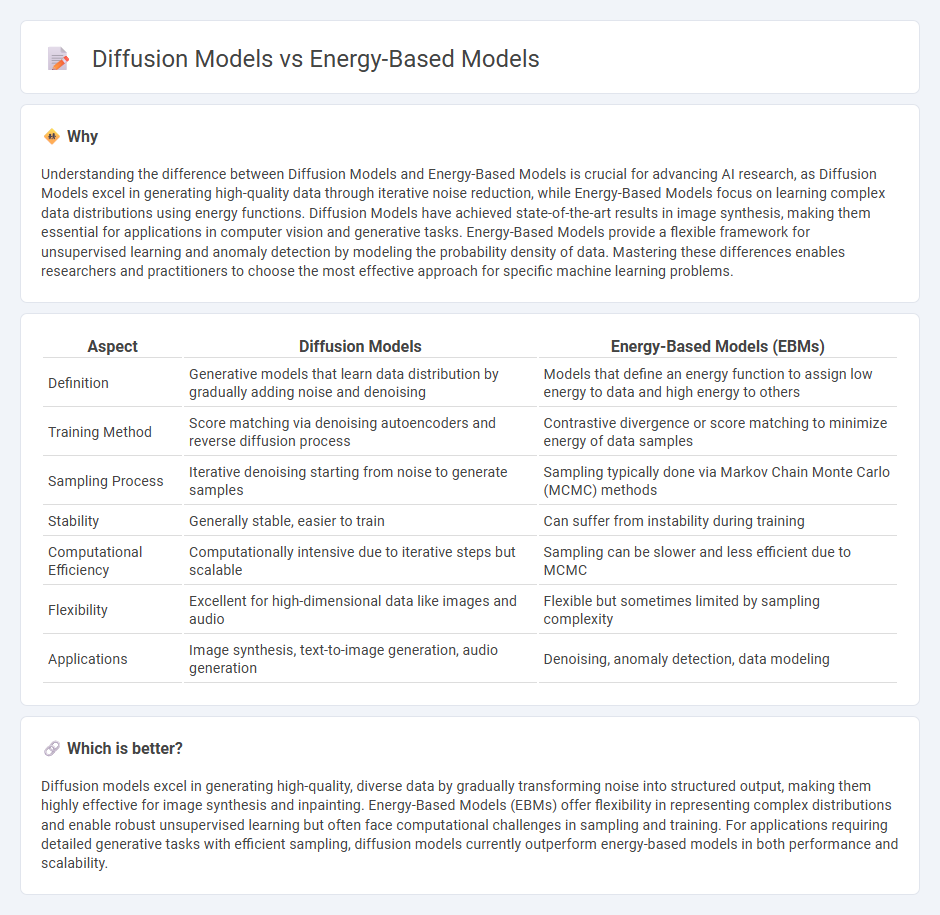
| Aspect | Diffusion Models | Energy-Based Models (EBMs) |
|---|---|---|
| Definition | Generative models that learn data distribution by gradually adding noise and denoising | Models that define an energy function to assign low energy to data and high energy to others |
| Training Method | Score matching via denoising autoencoders and reverse diffusion process | Contrastive divergence or score matching to minimize energy of data samples |
| Sampling Process | Iterative denoising starting from noise to generate samples | Sampling typically done via Markov Chain Monte Carlo (MCMC) methods |
| Stability | Generally stable, easier to train | Can suffer from instability during training |
| Computational Efficiency | Computationally intensive due to iterative steps but scalable | Sampling can be slower and less efficient due to MCMC |
| Flexibility | Excellent for high-dimensional data like images and audio | Flexible but sometimes limited by sampling complexity |
| Applications | Image synthesis, text-to-image generation, audio generation | Denoising, anomaly detection, data modeling |
Which is better?
Diffusion models excel in generating high-quality, diverse data by gradually transforming noise into structured output, making them highly effective for image synthesis and inpainting. Energy-Based Models (EBMs) offer flexibility in representing complex distributions and enable robust unsupervised learning but often face computational challenges in sampling and training. For applications requiring detailed generative tasks with efficient sampling, diffusion models currently outperform energy-based models in both performance and scalability.
Connection
Diffusion models and Energy-Based Models (EBMs) both represent complex data distributions through iterative refinement, with diffusion models gradually denoising data samples while EBMs define energy landscapes to capture data likelihood. They intersect in their reliance on stochastic processes and gradient-based sampling techniques, enabling efficient data generation and representation learning. This connection facilitates advancements in generative modeling, leveraging energy functions to enhance diffusion processes and improve sample quality.
Key Terms
Energy Function
Energy-Based Models define a scalar energy function to represent data compatibility, guiding the learning process via minimizing energy for observed data and maximizing for others. Diffusion Models utilize an energy function implicitly by modeling the data distribution through gradual noise addition and denoising steps, effectively learning the data manifold's structure. Discover more about how these energy functions influence model performance and applications.
Score Matching
Energy-Based Models (EBMs) leverage score matching to estimate data distributions by learning energy functions representing the data's probability landscape, enabling efficient sampling despite complex, high-dimensional inputs. Diffusion models apply score matching to iteratively denoise data through a learned gradient of the log-likelihood, effectively reversing a diffusion process that corrupts the data with noise. Explore deeper insights into how score matching bridges these models for advanced generative applications.
Stochastic Differential Equation
Energy-Based Models leverage an energy function to define probability distributions, often optimized through gradient-based methods, whereas Diffusion Models utilize Stochastic Differential Equations (SDEs) to progressively transform data distributions via forward and reverse diffusion processes. The SDEs in Diffusion Models characterize continuous-time stochastic processes enabling high-fidelity data generation by simulating noise perturbations and denoising trajectories. Explore more to understand how these mathematical frameworks empower generative modeling advances.
Source and External Links
Energy-based model - Wikipedia - Energy-based models (EBMs) are a class of generative models in machine learning that learn the characteristics of a dataset by assigning an energy value to each possible configuration, allowing them to estimate data distributions and generate new, similar data by minimizing energy for realistic samples.
Tutorial 8: Deep Energy-Based Generative Models - Energy-based models tackle the challenge of estimating complex, high-dimensional probability distributions over data (such as images) by using deep learning to assign higher likelihoods to realistic samples, avoiding the limitations of simple interpolation methods.
Energy-Based Models * Deep Learning - EBMs provide a flexible framework for learning and inference, allowing a wide range of choices in model architecture, training objectives, and handling of latent variables, with probabilities derived from energy functions via the Gibbs-Boltzmann distribution.
 dowidth.com
dowidth.com